题目内容
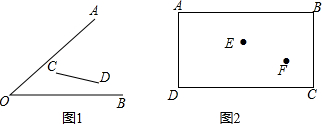
1.以边长为1的正方形ABCD的顶点A为圆心,以$\sqrt{2}$为半径作⊙A,则点C关于⊙A的位置关系是( )| A. | 点C 在⊙A内 | B. | 点C在⊙A上 | C. | 点C在⊙A外 | D. | 不能确定 |
分析 根据题意画出图形,由勾股定理求出AC的长,进而可得出结论.
解答  解:如图所示,
解:如图所示,
∵正方形ABCD的边长为1,
∴AC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$.
∵⊙A的半径为$\sqrt{2}$,
∴点C在⊙A上.
故选B.
点评 本题考查的是点与圆的位置关系,熟知点与圆的3种位置关系是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.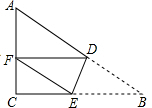 如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
 如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )| A. | $\frac{40}{9}$ | B. | $\frac{50}{9}$ | C. | $\frac{15}{4}$ | D. | $\frac{25}{4}$ |
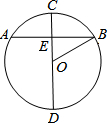 如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=8,则DE的长为8.
如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=8,则DE的长为8.