题目内容
5.已知3x+m=7,其中x≥0,求m的取值范围.分析 首先把3x+m=7变形为x=$\frac{7-m}{3}$,再根据x≥0可得$\frac{7-m}{3}$≥0,再解不等式即可.
解答 解:3x+m=7,
3x=7-m,
x=$\frac{7-m}{3}$,
∵x≥0,
∴$\frac{7-m}{3}$≥0,
解得:m≤7.
点评 此题主要考查了解一元一次不等式,关键是正确利用含m的式子表示x.

练习册系列答案
相关题目
15.-|(-1)100|等于( )
| A. | -100 | B. | 100 | C. | -1 | D. | 1 |
13.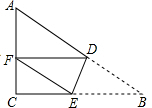 如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
 如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )| A. | $\frac{40}{9}$ | B. | $\frac{50}{9}$ | C. | $\frac{15}{4}$ | D. | $\frac{25}{4}$ |