题目内容
4.袋中装有除颜色外完全相同的2个红球和1个绿球.(1)现从袋中摸出1个球后放回,混合均匀后再摸出1个球.请用画树状图或列表的方法,求第一次摸到绿球,第二次摸到红球的概率;
(2)先从袋中摸出1个球后不放回,再摸出1个球,则两次摸到的球中有1个绿球和1个红球的概率是多少?请直接写出结果.
分析 (1)先画树状图展示所有9种等可能的结果数,再找出第一次摸到绿球,第二次摸到红球的结果数,然后根据概率公式求解;
(2)先画树状图展示所有6种等可能的结果数,再找出两次摸到的球中有1个绿球和1个红球的结果数,然后根据概率公式求解.
解答 解:(1)画树状图为:
共有9种等可能的结果数,其中第一次摸到绿球,第二次摸到红球的结果数为2,
所以第一次摸到绿球,第二次摸到红球的概率=$\frac{2}{9}$;
(2)画树状图为:
共有6种等可能的结果数,其中两次摸到的球中有1个绿球和1个红球的结果数为4,
所以两次摸到的球中有1个绿球和1个红球的概率=$\frac{4}{6}$=$\frac{2}{3}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.注意区分第一次摸了放回与不放回.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
14.已知函数y=2x2的图象是抛物线,现在同一坐标系中,将该抛物线分别向上、向左平移2个单位,那么所得到的新抛物线的解析式是( )
| A. | y=2(x+2)2+2 | B. | y=2(x+2)2-2 | C. | y=2(x-2)2-2 | D. | y=2(x-2)2+2 |
15.-|(-1)100|等于( )
| A. | -100 | B. | 100 | C. | -1 | D. | 1 |
13.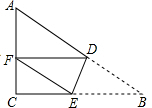 如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
 如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )| A. | $\frac{40}{9}$ | B. | $\frac{50}{9}$ | C. | $\frac{15}{4}$ | D. | $\frac{25}{4}$ |
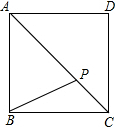 已知点P是正方形ABCD对角线AC上的一点,请探究线段PA,PC,PB的关系式,并写出证明过程.
已知点P是正方形ABCD对角线AC上的一点,请探究线段PA,PC,PB的关系式,并写出证明过程.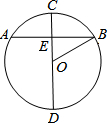 如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=8,则DE的长为8.
如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=8,则DE的长为8.