题目内容
18.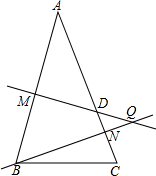 如图,在△ABC中,△ABC中,∠ABC=∠C,AB的垂直平分线MQ交AC于D,CD的垂直平分线恰好过点B,求∠A的度数.
如图,在△ABC中,△ABC中,∠ABC=∠C,AB的垂直平分线MQ交AC于D,CD的垂直平分线恰好过点B,求∠A的度数.
分析 连接BD,由线段垂直平分线的性质得出∠A=∠ABD,再由BQ是线段CD的垂直平分线得出BD=CD,故∠C=∠BDC,根据∠ABC=∠C可知∠ABC=∠BDC,故∠CBD=∠A,由此可得出BD是∠ABC的平分线,由三角形内角和定理即可得出结论.
解答 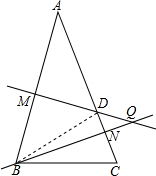 解:连接BD,
解:连接BD,
∵AB的垂直平分线MQ交AC于D,
∴∠A=∠ABD.
∵BQ是线段CD的垂直平分线,
∴BD=BC,
∴∠C=∠BDC.
∵∠ABC=∠C,
∴∠ABC=∠BDC,
∴∠CBD=∠A,
∴BD是∠ABC的平分线,
∴∠ABC=∠C=2∠A,
∵∠ABC+∠C+∠A=180°,即5∠A=180°,解得∠A=36°.
点评 本题考查的是线段垂直平分线的性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
13.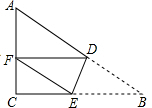 如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
 如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )| A. | $\frac{40}{9}$ | B. | $\frac{50}{9}$ | C. | $\frac{15}{4}$ | D. | $\frac{25}{4}$ |
3.
| 多项式 | 2x3y-4x2y2-3x5 | 2x-1 | 2x2-x-3 | x2-2x-4x3-1 |
| 项 | 2x3y,-4x2y2,-3x5 | 2x,-1 | 2x2,-x,-3 | x2,-2x,-4x3,-1 |
| 最高次项 | -3x5 | 2x | 2x2 | -4x3 |
| 常数项 | 0 | -1 | -3 | -1 |
| 几次几项式 | 五次三项式 | 一次二项式 | 二次三项式 | 三次四项式 |
 如图,AB是⊙0的直径,C、D是半圆的三等分点,则∠C+∠E+∠D=120°.
如图,AB是⊙0的直径,C、D是半圆的三等分点,则∠C+∠E+∠D=120°.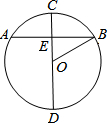 如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=8,则DE的长为8.
如图,⊙O的直径CD垂直弦AB于点E,且CE=2,AB=8,则DE的长为8.
 △ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交AC于点E,如果△ABC的周长为35,△BEC的周长为20,求BC的长.
△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交AC于点E,如果△ABC的周长为35,△BEC的周长为20,求BC的长.