题目内容
8.下列各式:1,a2+3ab+b2,-$\frac{1}{2}$x,xy,$\frac{1+x}{2}$,-$\frac{3{a}^{2}b}{2}$,πr4,x2-3x+1,其中单项式有1,-$\frac{1}{2}$x,xy,-$\frac{3{a}^{2}b}{2}$,πr4;多项式有a2+3ab+b2,x2-3x+1.分析 根据单项式和多项式的概念求解.
解答 解:单项式有:1,-$\frac{1}{2}$x,xy,-$\frac{3{a}^{2}b}{2}$,πr4;
多项式有:a2+3ab+b2,x2-3x+1.
故答案为:1,-$\frac{1}{2}$x,xy,-$\frac{3{a}^{2}b}{2}$,πr4;a2+3ab+b2,x2-3x+1.
点评 本题考查了单项式和多项式的概念:数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式;几个单项式的和叫做多项式.

练习册系列答案
相关题目
13.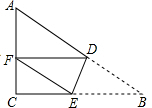 如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
 如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )| A. | $\frac{40}{9}$ | B. | $\frac{50}{9}$ | C. | $\frac{15}{4}$ | D. | $\frac{25}{4}$ |
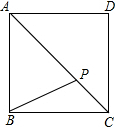 已知点P是正方形ABCD对角线AC上的一点,请探究线段PA,PC,PB的关系式,并写出证明过程.
已知点P是正方形ABCD对角线AC上的一点,请探究线段PA,PC,PB的关系式,并写出证明过程.
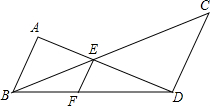 如图,已知AB∥EF∥CD,若AB=a,CD=b,EF=c,求证:$\frac{1}{c}=\frac{1}{a}+\frac{1}{b}$.
如图,已知AB∥EF∥CD,若AB=a,CD=b,EF=c,求证:$\frac{1}{c}=\frac{1}{a}+\frac{1}{b}$.