题目内容
3.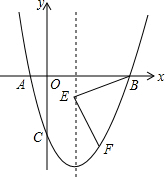 如图所示,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C,E为x轴下方的对称轴上一点且EF⊥BE交抛物线于F,且EB=EF,求点F坐标.
如图所示,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C,E为x轴下方的对称轴上一点且EF⊥BE交抛物线于F,且EB=EF,求点F坐标.
分析 作FH垂直抛物线的对称轴于H,对称轴交x轴于D,如图,利用抛物线与x轴的交点问题可求出A(-1,0),B(3,0),则抛物线的对称轴为直线x=1,所以BD2,再证明△BDE≌△EHF得到DE=HF,BD=EH=2,设F(t,t2-2t-3),则DH=-t2+2t+3,所以-t2+2t+3=t+1,然后解此方程求出t的值即可得到满足条件的F点的坐标.
解答 解:作FH垂直抛物线的对称轴于H,对称轴交x轴于D,如图,
当y=0时,x2-2x-3=0,解得x1=-1,x2=3,则A(-1,0),B(3,0),
∴抛物线的对称轴为直线x=1,
∴BD=3-1=2,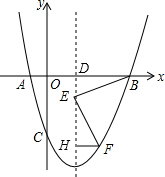
∵EF⊥BE,
∴∠BEF=90°,
∴∠BED+∠FEH=90°,
而∠BED+∠EBD=90°,
∴∠EBD=∠FEH,
在△BDE和△EHF中
$\left\{\begin{array}{l}{∠BDE=∠EHF}\\{∠EBD=∠FEH}\\{BE=EF}\end{array}\right.$,
∴△BDE≌△EHF,
∴DE=HF,BD=EH=2,
设F(t,t2-2t-3),则DH=-t2+2t+3,
而DH=DE+EH=HF+2=t-1+2=t+1,
∴-t2+2t+3=t+1,
整理得t2-t-2=0,解得t1=-1(舍去),t2=2,
∴F点的坐标为(2,-3).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了利用三角形全等解决线段相等的问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.已知函数y=2x2的图象是抛物线,现在同一坐标系中,将该抛物线分别向上、向左平移2个单位,那么所得到的新抛物线的解析式是( )
| A. | y=2(x+2)2+2 | B. | y=2(x+2)2-2 | C. | y=2(x-2)2-2 | D. | y=2(x-2)2+2 |
15.-|(-1)100|等于( )
| A. | -100 | B. | 100 | C. | -1 | D. | 1 |
13.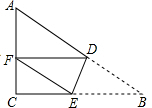 如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
 如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )
如图,△ABC中,∠C=90°,AC=6,BC=8,将△ABC沿DE折叠,使点B落在AC边上的F处,并且DF∥BC,则BD的长是( )| A. | $\frac{40}{9}$ | B. | $\frac{50}{9}$ | C. | $\frac{15}{4}$ | D. | $\frac{25}{4}$ |
 如图,AB是⊙0的直径,C、D是半圆的三等分点,则∠C+∠E+∠D=120°.
如图,AB是⊙0的直径,C、D是半圆的三等分点,则∠C+∠E+∠D=120°.