��Ŀ����
11��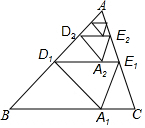 ��ͼ���ԡ�ABCֽƬ�������²�����
��ͼ���ԡ�ABCֽƬ�������²�������1�β���������ABC���Ź�AB�е�D1��ֱ���۵���ʹ��A����BC���ϵ�A1�����ۺ�D1E1��BC�ľ������h1��Ȼ��ԭֽƬ��
��2�β���������AD1E1���Ź�AD1�е�D2��ֱ���۵���ʹ��A����D1E1���ϵ�A1�����ۺ�D1E1��BC�ľ������h2��Ȼ��ԭֽƬ��
��
�������������ϲ�����ȥ����������n�β�����õ����ۺ�DnEn��BC�ľ������hn����h=1����hn��ֵ�������ǣ�������
| A�� | $\frac{3}{2}$ | B�� | $\frac{7}{4}$ | C�� | $\frac{13}{8}$ | D�� | $\frac{31}{16}$ |
���� �����е�����ʼ��۵������ʿɵ�DA=DA'=DB���Ӷ��ɵá�ADA'=2��B������۵������ʣ���ADA'=2��ADE���ɵá�ADE=��B���̶��ж�DE��BC���ó�DE�ǡ�ABC����λ�ߣ�֤��AA1��BC���õ�AA1=2�����h1=2-1=1��ͬ��h2=2-$\frac{1}{2}$�������õ��𰸣�
��� �⣺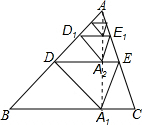 ����AA1��
����AA1��
���۵������ʿɵã�AA1��DE��DA=DA1��
�֡�D��AB�е㣬
��DA=DB��
��DB=DA1��
���BA1D=��B��
���ADA1=2��B��
�֡ߡ�ADA1=2��ADE��
���ADE=��B��
��DE��BC��
��AA1��BC��
��AA1=2��
��h1=2-1=1��
ͬ����h2=2-$\frac{1}{2}$��h3=2-$\frac{1}{{2}^{2}}$��
�ྭ����n�β�����õ����ۺ�Dn-1En-1��BC�ľ���hn=2-$\frac{1}{{2}^{n-1}}$��
��hn��ֵ��������$\frac{13}{8}$��
��ѡC��
���� ���⿼�������������ε��ж������ʣ���������λ�ߵ����ʣ�ƽ���ߵȷ��߶ζ������ҳ������ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
18����֪���κ���y=-3��x-h��2+5����x��-2ʱ��y��x���������С�����У�������
| A�� | h��-2 | B�� | h��-2 | C�� | h��-2 | D�� | h��-2 |
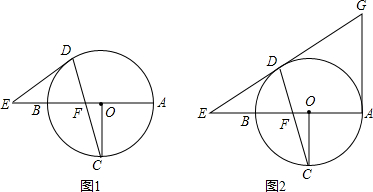
 ��ͼ���ھ���ABCD�У���O�ڶԽ���AB�ϣ���OA�ij�Ϊ�뾶��ԲO��AD���ڵ�E���ҡ�ACB=��DCE����֤��CE�ǡ�O�����ߣ�
��ͼ���ھ���ABCD�У���O�ڶԽ���AB�ϣ���OA�ij�Ϊ�뾶��ԲO��AD���ڵ�E���ҡ�ACB=��DCE����֤��CE�ǡ�O�����ߣ�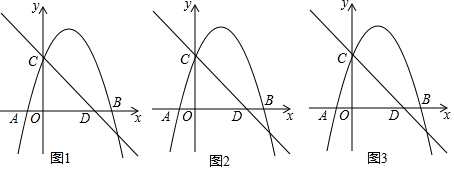
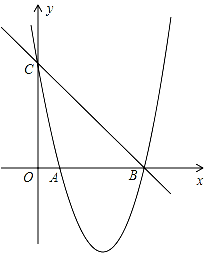 ��ͼ����֪������y=x2+bx+c��ͼ����x���һ������ΪB��5��0������һ������ΪA������y�ύ�ڵ�C��0��5����
��ͼ����֪������y=x2+bx+c��ͼ����x���һ������ΪB��5��0������һ������ΪA������y�ύ�ڵ�C��0��5����