题目内容
20.有下列六个数:0、1997、(-0.1)3、2.016、$\frac{13}{3}$、-$\frac{π}{5}$、0.3131131113…,若无理数的个数为x,整数的个数为y,非负数的个数为z,求x-y+z的平方根.分析 根据无理数、整数、非负数的个数,求出x、y、z的值,再根据平方根的定义解答即可.
解答 解:无理数:$-\frac{π}{5}$、0.3131131113…,故x=2,
整数:0、1997,故y=2,
非负数:0、1997、2.016、$\frac{13}{3}$、0.3131131113…,故z=5,
∴x-y+z=2-2+5=5,
∴x-y+z的平方根为$±\sqrt{5}$.
点评 本题主要考查实数的分类、平方根的定义,实数包括有理数和无理数;实数可分为正数、负数和0;正数的平方根由两个,且互为相反数.

练习册系列答案
相关题目
11.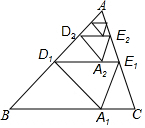 如图,对△ABC纸片进行如下操作:
如图,对△ABC纸片进行如下操作:
第1次操作:将△ABC沿着过AB中点D1的直线折叠,使点A落在BC边上的A1处,折痕D1E1到BC的距离记作h1,然后还原纸片;
第2次操作:将△AD1E1沿着过AD1中点D2的直线折叠,使点A落在D1E1边上的A1处,折痕D1E1到BC的距离记作h2,然后还原纸片;
…
按上述方法不断操作下去…,经过第n次操作后得到的折痕DnEn到BC的距离记作hn,若h=1,则hn的值不可能是( )
 如图,对△ABC纸片进行如下操作:
如图,对△ABC纸片进行如下操作:第1次操作:将△ABC沿着过AB中点D1的直线折叠,使点A落在BC边上的A1处,折痕D1E1到BC的距离记作h1,然后还原纸片;
第2次操作:将△AD1E1沿着过AD1中点D2的直线折叠,使点A落在D1E1边上的A1处,折痕D1E1到BC的距离记作h2,然后还原纸片;
…
按上述方法不断操作下去…,经过第n次操作后得到的折痕DnEn到BC的距离记作hn,若h=1,则hn的值不可能是( )
| A. | $\frac{3}{2}$ | B. | $\frac{7}{4}$ | C. | $\frac{13}{8}$ | D. | $\frac{31}{16}$ |
8.计算:
(1)(-1)2017-23+(cos68°+$\frac{5}{π}$)0+|3$\sqrt{3}$-8sin60°|;
(2)$\sqrt{2}$cos45°-tan30°•sin60°.
(1)(-1)2017-23+(cos68°+$\frac{5}{π}$)0+|3$\sqrt{3}$-8sin60°|;
(2)$\sqrt{2}$cos45°-tan30°•sin60°.
15.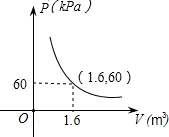 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )| A. | 不小于$\frac{5}{4}$ m3 | B. | 小于$\frac{5}{4}$ m3 | C. | 不小于$\frac{4}{5}$ m3 | D. | 小于$\frac{4}{5}$ m3 |
2.某次篮球联赛共有十支队伍参赛,部分积分表如下:
其中一队的胜场总积分能否等于负场总积分?请说明理由.
| 队名 | 比赛场次 | 胜场 | 负场 | 积分 |
| A | 16 | 12 | 4 | 28 |
| B | 16 | 10 | 6 | 26 |
| C | 16 | 8 | 8 | 24 |
| D | 16 | 0 | 16 | 16 |
6.若k为正整数,则2•(-2)2k+(-2)2k+1等于( )
| A. | 0 | B. | 22k+1 | C. | -22k+1 | D. | 22k+2 |