题目内容
观察图形,解答问题:
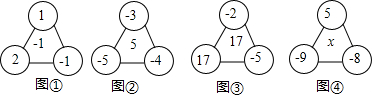
(1)按下表已填写的形式填写表中的空格:
(2)请用你发现的规律,求出图④中的数x.

(1)按下表已填写的形式填写表中的空格:
| 图① | 图② | 图③ | |
| 三个角上三个数的积 | 1×(-1)×2=-2 | (-3)×(-4)×(-5)=-60 | |
| 三个角上三个数的和 | 1+(-1)+2=2 | (-3)+(-4)+(-5)=-12 | |
| 三个数与中间数字的积 | 2×(-1)=-2 |
考点:规律型:图形的变化类
专题:
分析:(1)根据图形和表中已填写的形式,即可求出表中的空格;
(2)根据图①②③可知,中间的数是三个角上的数字的乘积与和的商,列出方程,即可求出x的值.
(2)根据图①②③可知,中间的数是三个角上的数字的乘积与和的商,列出方程,即可求出x的值.
解答:解:(1)②(-12)×5=-60
③(-2)×17×(-5)=170
(-2)+17+(-5)=10
10×17=170
(2)[5+(-8)+(-9)]x=5×(-8)×(-9)
解得,x=-30.
③(-2)×17×(-5)=170
(-2)+17+(-5)=10
10×17=170
(2)[5+(-8)+(-9)]x=5×(-8)×(-9)
解得,x=-30.
点评:此题考查了数字的变化类,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.

练习册系列答案
相关题目
若抛物线y=x2-4x+3-t(t为实数)在0<x<3
的范围内与x轴有公共点,则t的取值范围为( )
| 1 |
| 2 |
| A、-1<t<3 | ||
| B、-1≤t<3 | ||
C、
| ||
| D、t≥-1 |
 小花用围棋子摆正方形,第1,2,3,4个分别如图所示,按这样的规律往下摆,第10个正方形需要的棋子枚数是( )
小花用围棋子摆正方形,第1,2,3,4个分别如图所示,按这样的规律往下摆,第10个正方形需要的棋子枚数是( )| A、44枚 | B、40枚 |
| C、36枚 | D、32枚 |
 如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为640m2的矩形临时仓库,仓库一边靠墙,另三边用总长为80m的栅栏围成,若设栅栏AB的长为xm,则下列各方程中,符合题意的是( )
如图所示,在一边靠墙(墙足够长)的空地上,修建一个面积为640m2的矩形临时仓库,仓库一边靠墙,另三边用总长为80m的栅栏围成,若设栅栏AB的长为xm,则下列各方程中,符合题意的是( )A、
| ||
B、
| ||
| C、x(80-2x)=640 | ||
| D、x(80-x)=640 |
抛物线y=-x2+2x+2绕它与y轴的交点旋转180°后得到的抛物线解析式为( )
| A、y=x2+2x+2 |
| B、y=-x2-2x+2 |
| C、y=x2+2x+1 |
| D、y=2x2+4x+2 |
 已知:BE⊥CD,BE=DE,BC=DA,求证:∠B=∠D.
已知:BE⊥CD,BE=DE,BC=DA,求证:∠B=∠D. 如图,直线L⊥n,作一条直线,使它与直线L、n围成的直角三角形的面积是6,且这个直角三角形的一条直角边为3,则这样的直线最多可以作
如图,直线L⊥n,作一条直线,使它与直线L、n围成的直角三角形的面积是6,且这个直角三角形的一条直角边为3,则这样的直线最多可以作