题目内容
 已知:BE⊥CD,BE=DE,BC=DA,求证:∠B=∠D.
已知:BE⊥CD,BE=DE,BC=DA,求证:∠B=∠D.考点:全等三角形的判定与性质
专题:证明题
分析:由BE⊥CD就可以得出∠BEC=∠BED=90°,再由条件证明Rt△BEC≌Rt△DEA就可以得出结论.
解答:证明:∵BE⊥CD,
∴∠BEC=∠BED=90°.
在Rt△BEC和Rt△DEA中
∴Rt△BEC≌Rt△DEA(HL),
∴∠B=∠D.
∴∠BEC=∠BED=90°.
在Rt△BEC和Rt△DEA中
|
∴Rt△BEC≌Rt△DEA(HL),
∴∠B=∠D.
点评:本题考查了直角三角形的判定的运用,全等三角形判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
某小组同学聚会,见面时相互间均握了一次手,好事者统计:一共握了36次.你认为这次聚会的同学有( )人.
| A、7 | B、8 | C、9 | D、10 |
若抛物线y=ax2+bx+c的对称轴是x=-2,则
等于( )
| a |
| b |
| A、2 | ||
B、
| ||
| C、4 | ||
D、
|
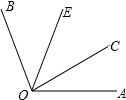 如图,OC是∠AOB内部的一条射线,∠AOC=32°,OE是∠COB的平分线.已知∠COE=43°,则∠AOB=
如图,OC是∠AOB内部的一条射线,∠AOC=32°,OE是∠COB的平分线.已知∠COE=43°,则∠AOB= 如图是某个几何体的表面展开图,那么这个几何体是
如图是某个几何体的表面展开图,那么这个几何体是 如图,点D、E是等边△ABC的BC、AC上的点,且CD=AE,AD、BE相交于P点,BQ⊥AD.
如图,点D、E是等边△ABC的BC、AC上的点,且CD=AE,AD、BE相交于P点,BQ⊥AD. 如图,已知点A、D、C、F在同一条直线上,AB=DE,∠B=∠E,要使△ABC≌△DEF,还需要添加一个条件是
如图,已知点A、D、C、F在同一条直线上,AB=DE,∠B=∠E,要使△ABC≌△DEF,还需要添加一个条件是