题目内容
 如图,直线L⊥n,作一条直线,使它与直线L、n围成的直角三角形的面积是6,且这个直角三角形的一条直角边为3,则这样的直线最多可以作
如图,直线L⊥n,作一条直线,使它与直线L、n围成的直角三角形的面积是6,且这个直角三角形的一条直角边为3,则这样的直线最多可以作考点:三角形的面积
专题:
分析:分四种情况分别讨论即可求得:当AC在直线L上,且在直线n的上方时有两条;当AC在直线L上,且在直线n的下方时存在两条;当AC在直线n上,且在直线L的左边时,可以作两条,当AC在直线n上,且在直线L的右边时,又可以作两条;从而可以判断直线的条数.
解答:解:设围成的直角三角形为△ABC,∠ACB=90°,AC=3,
∵三角形的面积是6,
∴BC=4,
∴AB=5,
当AC在直线L上,且在直线n的上方时,以A为圆心以5为半径作圆交直线n两点,连接A和交点得到两个面积为6的直角三角形,故可以作两条;
当AC在直线L上,且在直线n的下方时,以A为圆心以5为半径作圆交直线n两点,连接A和交点得到两个面积为6的直角三角形,故又可以作两条;
同理:当AC在直线n上,且在直线L的左边时,可以作两条,当AC在直线n上,且在直线L的右边时,又可以作两条;
故可以作8条,
故答案为8.
∵三角形的面积是6,
∴BC=4,
∴AB=5,
当AC在直线L上,且在直线n的上方时,以A为圆心以5为半径作圆交直线n两点,连接A和交点得到两个面积为6的直角三角形,故可以作两条;
当AC在直线L上,且在直线n的下方时,以A为圆心以5为半径作圆交直线n两点,连接A和交点得到两个面积为6的直角三角形,故又可以作两条;
同理:当AC在直线n上,且在直线L的左边时,可以作两条,当AC在直线n上,且在直线L的右边时,又可以作两条;
故可以作8条,
故答案为8.
点评:本题考查了三角形的面积以及勾股定理的应用,熟练掌握三角形的面积公式是解题的关键.

练习册系列答案
相关题目
下列图案均是用长度相同的小木棒按一定的规律拼搭而成:拼搭第1个图案需4根小木棒,拼塔第2个图案需10根小木棒,…,依此规律,拼成第6个图案小木棒( )


| A、36根 | B、48根 |
| C、54根 | D、64根 |
某小组同学聚会,见面时相互间均握了一次手,好事者统计:一共握了36次.你认为这次聚会的同学有( )人.
| A、7 | B、8 | C、9 | D、10 |
 如图,在Rt△ACB中,∠ACB=90°,点D是AB上一点.将△BCD沿CD折叠,使B点落在AC边上的B′处.
如图,在Rt△ACB中,∠ACB=90°,点D是AB上一点.将△BCD沿CD折叠,使B点落在AC边上的B′处. 如图,点D、E是等边△ABC的BC、AC上的点,且CD=AE,AD、BE相交于P点,BQ⊥AD.
如图,点D、E是等边△ABC的BC、AC上的点,且CD=AE,AD、BE相交于P点,BQ⊥AD.
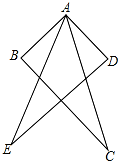 如图,AB=AD,AE=AC,∠BAE=∠DAC,求证:BC=DE.
如图,AB=AD,AE=AC,∠BAE=∠DAC,求证:BC=DE.