题目内容
直线y=x-2与抛物线y=ax2+bx+c相交于(2,m),(n,3)两点,抛物线的对称轴是直线x=3,
(1)求抛物线的关系式和顶点坐标;
(2)将此抛物线水平平移几个单位,可使抛物线顶点在直线y=x-2上?
(1)求抛物线的关系式和顶点坐标;
(2)将此抛物线水平平移几个单位,可使抛物线顶点在直线y=x-2上?
考点:二次函数图象与几何变换
专题:计算题
分析:(1)把(2,m),(n,3)分别代入y=x-2可求出m和n,即可得到点(2,0)、(5,3)在抛物线y=ax2+bx+c上,利用抛物线的对称性得到抛物线与x轴的另一个交点坐标为(4,0),则可设交点式y=a(x-2)(x-4),然后把(5,3)代入可计算出a=1,即可得到抛物线解析式为y=x2-6x+8,再配成顶点式y=(x-3)2-1,于是得到抛物线的顶点坐标为(3,-1);
(2)由于顶点水平平移,纵坐标不变,通过计算得到点(1,-1)在直线y=x-2上,而顶点(3,-1)向左平移2个单位得到点(1,-1),于是将抛物线y=x2-6x+8向左平移2个单位,可使抛物线顶点在直线y=x-2上.
(2)由于顶点水平平移,纵坐标不变,通过计算得到点(1,-1)在直线y=x-2上,而顶点(3,-1)向左平移2个单位得到点(1,-1),于是将抛物线y=x2-6x+8向左平移2个单位,可使抛物线顶点在直线y=x-2上.
解答:解:(1)把(2,m),(n,3)分别代入y=x-2得m=2-2=0,n-2=3,解得n=5,即点(2,0)、(5,3)在抛物线y=ax2+bx+c上,
由于抛物线的对称轴是直线x=3,则抛物线与x轴的另一个交点坐标为(4,0),
设抛物线的解析式为y=a(x-2)(x-4),
把(5,3)代入得a•3•1=3,解得a=1,
所以抛物线解析式为y=(x-2)(x-4)=x2-6x+8,
由于y=(x-3)2-1,
所以抛物线的顶点坐标为(3,-1);
(2)当y=-1时,x-2=-1,解得x=1,即点(1,-1)在直线y=x-2上,
把顶点(3,-1)向左平移2个单位得到点(1,-1),这样抛物线的顶点在直线y=x-2上,
所以将抛物线y=x2-6x+8向左平移2个单位,可使抛物线顶点在直线y=x-2上.
由于抛物线的对称轴是直线x=3,则抛物线与x轴的另一个交点坐标为(4,0),
设抛物线的解析式为y=a(x-2)(x-4),
把(5,3)代入得a•3•1=3,解得a=1,
所以抛物线解析式为y=(x-2)(x-4)=x2-6x+8,
由于y=(x-3)2-1,
所以抛物线的顶点坐标为(3,-1);
(2)当y=-1时,x-2=-1,解得x=1,即点(1,-1)在直线y=x-2上,
把顶点(3,-1)向左平移2个单位得到点(1,-1),这样抛物线的顶点在直线y=x-2上,
所以将抛物线y=x2-6x+8向左平移2个单位,可使抛物线顶点在直线y=x-2上.
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
若∠A=20°18′,∠B=20°15″,∠C=20.25°,则有( )
| A、∠A>∠B>∠C |
| B、∠B>∠A>∠C |
| C、∠A>∠C>∠B |
| D、∠C>∠A>∠B |
 如图,OC平分∠AOB,如果∠AOB=36°,则∠AOC=
如图,OC平分∠AOB,如果∠AOB=36°,则∠AOC= 如图,在Rt△ACB中,∠ACB=90°,点D是AB上一点.将△BCD沿CD折叠,使B点落在AC边上的B′处.
如图,在Rt△ACB中,∠ACB=90°,点D是AB上一点.将△BCD沿CD折叠,使B点落在AC边上的B′处. 如图是某个几何体的表面展开图,那么这个几何体是
如图是某个几何体的表面展开图,那么这个几何体是 如图,点D、E是等边△ABC的BC、AC上的点,且CD=AE,AD、BE相交于P点,BQ⊥AD.
如图,点D、E是等边△ABC的BC、AC上的点,且CD=AE,AD、BE相交于P点,BQ⊥AD.
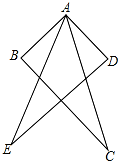 如图,AB=AD,AE=AC,∠BAE=∠DAC,求证:BC=DE.
如图,AB=AD,AE=AC,∠BAE=∠DAC,求证:BC=DE.