题目内容
12.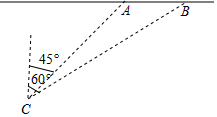 小陈站在小河AB一侧的C处(小河的宽度忽略不计),9:00测得小船在其北偏东45°的A处向正东方向航行,11:00又测得小船在其北偏东60°的B处,若小陈站的位置到小河的距离是200千米,求小船的航行速度(精确到个位).参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73.
小陈站在小河AB一侧的C处(小河的宽度忽略不计),9:00测得小船在其北偏东45°的A处向正东方向航行,11:00又测得小船在其北偏东60°的B处,若小陈站的位置到小河的距离是200千米,求小船的航行速度(精确到个位).参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73.
分析 先过C作CD⊥AB于D,根据△ACD是等腰直角三角形,得到AD=CD=200,再根据∠BCD=60°,得出tan60°=$\frac{DB}{CD}$,即$\frac{200+AB}{200}$=$\sqrt{3}$,进而得到AB=200($\sqrt{3}$-1),再根据小船的航行时间为2小时,即可得到小船的航行速度.
解答  解:如图所示,过C作CD⊥AB于D,
解:如图所示,过C作CD⊥AB于D,
∵∠ACD=45°,
∴△ACD是等腰直角三角形,
∴AD=CD=200,
∵∠BCD=60°,
∴tan60°=$\frac{DB}{CD}$,即$\frac{200+AB}{200}$=$\sqrt{3}$,
解得AB=200($\sqrt{3}$-1),
∴小船的航行速度为:200($\sqrt{3}$-1)÷2=100($\sqrt{3}$-1)≈73千米/小时.
点评 本题主要考查了解直角三角形的应用,在解决有关方向角的问题中,一般要根据题意理清图形中各角的关系,有时所给的方向角并不一定在直角三角形中,需要用到两直线平行内错角相等或一个角的余角等知识转化为所需要的角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2. 王博在做课外习题时遇到如图所示一道题,其中
王博在做课外习题时遇到如图所示一道题,其中 是被污损而看不清的一个数,它翻看答案后得知该题的计算结果为15,则
是被污损而看不清的一个数,它翻看答案后得知该题的计算结果为15,则 表示的数是( )
表示的数是( )
 王博在做课外习题时遇到如图所示一道题,其中
王博在做课外习题时遇到如图所示一道题,其中 是被污损而看不清的一个数,它翻看答案后得知该题的计算结果为15,则
是被污损而看不清的一个数,它翻看答案后得知该题的计算结果为15,则 表示的数是( )
表示的数是( )| A. | 10 | B. | -4 | C. | -10 | D. | 10或-4 |
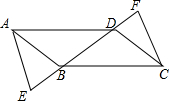 如图,在四边形ABCD中,已知AB=DC,AD=BC,点E,F在直线BD上,且BE=DF.
如图,在四边形ABCD中,已知AB=DC,AD=BC,点E,F在直线BD上,且BE=DF.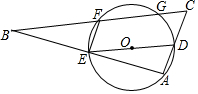 如图,已知ED为⊙O的直径且ED=4,点A(不与E、D重合)为⊙O上一个动点,线段AB经过点E,且EA=EB,F为⊙O上一点,∠FEB=90°,BF的延长线交AD的延长线交于点C.
如图,已知ED为⊙O的直径且ED=4,点A(不与E、D重合)为⊙O上一个动点,线段AB经过点E,且EA=EB,F为⊙O上一点,∠FEB=90°,BF的延长线交AD的延长线交于点C. 如图所示,在四边形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
如图所示,在四边形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).