题目内容
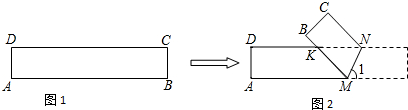
1. 如图所示,在四边形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).
如图所示,在四边形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).(1)设△DPQ的面积为S,请用含t的式子表示S;
(2)当t为何值时,PCDQ为平行四边形;
(3)当t为何值时,PD=PQ.
分析 (1)由题意得出AQ=t,DQ=16-t,△DPQ的面积S=$\frac{1}{2}$DQ•AB,即可得出S与t之间的函数关系式;
(2)若四边形PCDQ是平行四边形,则DQ=PC,得出方程,解方程即可;
(3)作PE⊥AD于E,则四边形ABPE是矩形,得出AE=PB,由PD=PQ,得出PE垂直平分DQ,求出QD、DE,得出AE,列出方程,解方程即可.
解答 解:(1)根据题意得:AQ=t,
∴DQ=16-t,
∴△DPQ的面积S=$\frac{1}{2}$×(16-t)×12=96-6t,
即S与t之间的函数关系式为:S=96-6t;
(2)∵PB=2t,
∴PC=21-2t,
若四边形PCDQ是平行四边形,
则DQ=PC,
∴16-t=21-2t,
解得:t=5,
∴当t=5时,四边形PCDQ是平行四边形;
(3)作PE⊥AD于E,如图所示: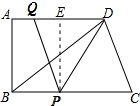 则四边形ABPE是矩形,
则四边形ABPE是矩形,
∴AE=PB,
∵PD=PQ,
∴QE=DE=$\frac{1}{2}$QD,
∵AQ=t,PB=2t,
∴QD=16-t,
∴DE=$\frac{1}{2}$(16-t),
∴AE=AD-DE=16-$\frac{1}{2}$(16-t)=8+$\frac{1}{2}$t,
∴8+$\frac{1}{2}$t=2t,
解得:t=$\frac{16}{3}$,
∴t=$\frac{16}{3}$时,PD=PQ.
点评 本题是四边形综合题目,考查了直角梯形的性质、平行四边形的性质、矩形的判定与性质、线段垂直平分线的性质、三角形面积的计算等知识;本题有一定难度,综合性强,特别是(4)中,需要通过作辅助线运用矩形的性质列出方程才能得出结果.

练习册系列答案
相关题目
9.下列哪个点在函数y=3-2x的图象上( )
| A. | (3,-2) | B. | (0,$\frac{3}{2}$) | C. | (3,0) | D. | ($\frac{3}{2}$,0) |
16.已知点A(0,2),B(4,4),点M在x轴上,当AM+BM最小时,点M的坐标为( )
| A. | (1,0) | B. | ($\frac{4}{3}$,0) | C. | ($\sqrt{2}$,0) | D. | (2,0) |
6. 已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )
已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )
 已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )
已知△ABC在正方形网格中的位置如图所示,点A、B、C、P均在格点上,则点P叫做△ABC的( )| A. | 内心 | B. | 重心 | C. | 外心 | D. | 无法确定 |
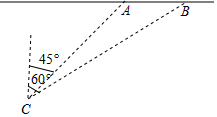 小陈站在小河AB一侧的C处(小河的宽度忽略不计),9:00测得小船在其北偏东45°的A处向正东方向航行,11:00又测得小船在其北偏东60°的B处,若小陈站的位置到小河的距离是200千米,求小船的航行速度(精确到个位).参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73.
小陈站在小河AB一侧的C处(小河的宽度忽略不计),9:00测得小船在其北偏东45°的A处向正东方向航行,11:00又测得小船在其北偏东60°的B处,若小陈站的位置到小河的距离是200千米,求小船的航行速度(精确到个位).参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73.