题目内容
7.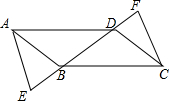 如图,在四边形ABCD中,已知AB=DC,AD=BC,点E,F在直线BD上,且BE=DF.
如图,在四边形ABCD中,已知AB=DC,AD=BC,点E,F在直线BD上,且BE=DF.(1)求证:△ABD≌△CDB;
(2)求证:∠E=∠F;
(3)请说明AE与CF的关系.
分析 (1)根据SSS即可证明;
(2)只要证明△ABE≌△CDF即可解决问题.
(3)结论:AE=CF,AE∥CF,利用(2)中结论即可证明.
解答 (1)证明:在△ABD和△CDB中,
$\left\{\begin{array}{l}{AB=CD}\\{AD=BC}\\{BD=DB}\end{array}\right.$,
∴△ABD≌△CDB.
(2)∵△ABD≌△CDB,
∴∠ABD=∠BDC,
∴∠ABE=∠CDF,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{AB=CD}\\{∠ABE=∠CDF}\\{BE=DF}\end{array}\right.$,
∴△ABE≌△CDF,
∴∠E=∠F.
(3)结论:AE∥CF,AE=CF.
∵△ABE≌△CDF,
∴∠E=∠F.AE=CF,
∴AE∥CF.
点评 本题考查全等三角形的判定和性质,解题的关键是灵活运用全等三角形的判定方法,正确寻找全等的条件,属于中考常考题型.

练习册系列答案
相关题目
16.已知点A(0,2),B(4,4),点M在x轴上,当AM+BM最小时,点M的坐标为( )
| A. | (1,0) | B. | ($\frac{4}{3}$,0) | C. | ($\sqrt{2}$,0) | D. | (2,0) |
 如图,将小正方体切去一个角后再展开,其平面展开图正确的是( )
如图,将小正方体切去一个角后再展开,其平面展开图正确的是( )



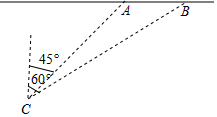 小陈站在小河AB一侧的C处(小河的宽度忽略不计),9:00测得小船在其北偏东45°的A处向正东方向航行,11:00又测得小船在其北偏东60°的B处,若小陈站的位置到小河的距离是200千米,求小船的航行速度(精确到个位).参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73.
小陈站在小河AB一侧的C处(小河的宽度忽略不计),9:00测得小船在其北偏东45°的A处向正东方向航行,11:00又测得小船在其北偏东60°的B处,若小陈站的位置到小河的距离是200千米,求小船的航行速度(精确到个位).参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73. 如图,在等腰三角形ABC中,∠ACB=90°,O是AC中点,D在OB上,且OA=OD,AD的延长线交BC于E,连接CD.
如图,在等腰三角形ABC中,∠ACB=90°,O是AC中点,D在OB上,且OA=OD,AD的延长线交BC于E,连接CD.