题目内容
17.把抛物线y=-$\frac{1}{2}{x^2}$经( )平移得到y=-$\frac{1}{2}{(x-2)^2}$-1.| A. | 向右平移2个单位,向上平移1个单位 | |
| B. | 向右平移2个单位,向下平移1个单位 | |
| C. | 向左平移2个单位,向上平移1个单位 | |
| D. | 向左平移2个单位,向下平移1个单位 |
分析 根据两抛物线的顶点坐标的平移规律得到抛物线的平移规律.
解答 解:∵抛物线y=-$\frac{1}{2}{x^2}$的顶点坐标是(0,0),抛物线y=-$\frac{1}{2}{(x-2)^2}$-1的顶点坐标是(2,-1),
∴由点(0,0)向右平移2个单位,向下平移1个单位得到点(2,-1),
∴把抛物线y=-$\frac{1}{2}{x^2}$经向右平移2个单位,向下平移1个单位得到y=-$\frac{1}{2}{(x-2)^2}$-1.
故选:B.
点评 主要考查了函数图象的平移,抛物线与坐标轴的交点坐标的求法,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
7.如果两个相似三角形相似比是1:4,那么它们的对应角平分线之比是( )
| A. | 1:4 | B. | 1:8 | C. | 1:16 | D. | 1:2 |
8. 如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAB:∠DAC=4:3,则∠EFC的度数为( )
如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAB:∠DAC=4:3,则∠EFC的度数为( )
 如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAB:∠DAC=4:3,则∠EFC的度数为( )
如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAB:∠DAC=4:3,则∠EFC的度数为( )| A. | 30° | B. | 40° | C. | 70° | D. | 80° |
5.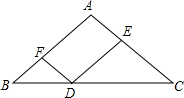 如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是( )
如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是( )
 如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是( )
如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是( )| A. | 24 | B. | 18 | C. | 16 | D. | 12 |
12.下列各长度的三条线段能组成三角形的是( )
| A. | 5、3、9 | B. | 5、3、8 | C. | 5、2、7 | D. | 5、3、6 |
2.在-2,+3.5,0,$\frac{2}{3}$,-0.7,11中,负数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
9. 如图是几何体的三视图,该几何体是( )
如图是几何体的三视图,该几何体是( )
 如图是几何体的三视图,该几何体是( )
如图是几何体的三视图,该几何体是( )| A. | 圆锥 | B. | 圆柱 | C. | 正三棱柱 | D. | 正三棱锥 |
6. 如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
 如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )| A. | OA=OC,OB=OD | B. | AB=CD,AO=CO | C. | AD∥BC,AD=BC | D. | ∠BAD=∠BCD,AB∥CD |
7.如果分式$\frac{2x}{x+3}$有意义,那么x的取值范围是( )
| A. | x≠0 | B. | x≤-3 | C. | x≥-3 | D. | x≠-3 |