题目内容
16.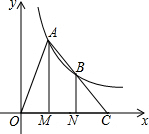 如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
分析 由BN∥AM可判断△CNB∽△CMA,根据相似的性质得S△CNB:S△CMA=($\frac{CN}{CM}$)2=$\frac{1}{4}$,则S△CMA=8,由于OM=MN=NC,根据三角形面积公式得到S△AOM=$\frac{1}{2}$S△AMC=4,然后根据反比例函数k的几何意义得到S△AOM=$\frac{1}{2}$|k|=4,再去绝对值易得k的值.
解答  解:∵BN∥AM,MN=NC,
解:∵BN∥AM,MN=NC,
∴△CNB∽△CMA,
∴S△CNB:S△CMA=($\frac{CN}{CM}$)2=($\frac{1}{2}$)2=$\frac{1}{4}$,而S△BNC=2,
∴S△CMA=8,
∵OM=MN=NC,
∴OM=$\frac{1}{2}$MC,
∴S△AOM=$\frac{1}{2}$S△AMC=4,
∵S△AOM=$\frac{1}{2}$|k|,
∴$\frac{1}{2}$|k|=4,
∴k=8.
故选(C)
点评 本题主要考查了反比例函数的比例系数k的几何意义以及相似三角形的判定与性质.从反比例函数y=$\frac{k}{x}$(k≠0)图象上任意一点向x轴或y轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.铅球的左视图是( )
| A. | 圆 | B. | 长方形 | C. | 正方形 | D. | 三角形 |
7.如果两个相似三角形相似比是1:4,那么它们的对应角平分线之比是( )
| A. | 1:4 | B. | 1:8 | C. | 1:16 | D. | 1:2 |
4. 如图,已知AB∥CD∥EF,则x、y、z三者之间的关系是( )
如图,已知AB∥CD∥EF,则x、y、z三者之间的关系是( )
 如图,已知AB∥CD∥EF,则x、y、z三者之间的关系是( )
如图,已知AB∥CD∥EF,则x、y、z三者之间的关系是( )| A. | x+y+z=180° | B. | x+y-z=180° | C. | y-x-z=0° | D. | y-x-2z=0° |
11.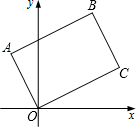 将矩形OABC如图放置,O为原点.若点A(-1,2),点B的纵坐标是$\frac{7}{2}$,则点C的坐标是( )
将矩形OABC如图放置,O为原点.若点A(-1,2),点B的纵坐标是$\frac{7}{2}$,则点C的坐标是( )
 将矩形OABC如图放置,O为原点.若点A(-1,2),点B的纵坐标是$\frac{7}{2}$,则点C的坐标是( )
将矩形OABC如图放置,O为原点.若点A(-1,2),点B的纵坐标是$\frac{7}{2}$,则点C的坐标是( )| A. | (4,2) | B. | (2,4) | C. | ($\frac{3}{2}$,3) | D. | (3,$\frac{3}{2}$) |
1. 菱形ABCD的两条对角线相交于O,若AC=6,BD=8,则菱形ABCD的周长是( )
菱形ABCD的两条对角线相交于O,若AC=6,BD=8,则菱形ABCD的周长是( )
 菱形ABCD的两条对角线相交于O,若AC=6,BD=8,则菱形ABCD的周长是( )
菱形ABCD的两条对角线相交于O,若AC=6,BD=8,则菱形ABCD的周长是( )| A. | $4\sqrt{3}$ | B. | 20 | C. | 24 | D. | $2\sqrt{3}$ |
8. 如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAB:∠DAC=4:3,则∠EFC的度数为( )
如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAB:∠DAC=4:3,则∠EFC的度数为( )
 如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAB:∠DAC=4:3,则∠EFC的度数为( )
如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAB:∠DAC=4:3,则∠EFC的度数为( )| A. | 30° | B. | 40° | C. | 70° | D. | 80° |
5.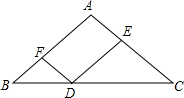 如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是( )
如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是( )
 如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是( )
如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是( )| A. | 24 | B. | 18 | C. | 16 | D. | 12 |
6. 如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
 如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )| A. | OA=OC,OB=OD | B. | AB=CD,AO=CO | C. | AD∥BC,AD=BC | D. | ∠BAD=∠BCD,AB∥CD |