题目内容
13．
如图所示的△ABC中，∠ABC=90°，∠ACB=40°，AC∥BD，∠ABD=（ ）| A． | 40° | B． | 50° | C． | 140° | D． | 130° |
分析 根据直角三角形两锐角互余的性质求出∠A，再根据两直线平行，内错角相等解答．
解答 解：∵∠ABC=90°，∠C=40°，
∴∠A=90°-∠C=90°-40°=50°，
∵BD∥AC，
∴∠ABD=∠A=50°．
故选：B．
点评 本题考查了两直线平行，内错角相等的性质，直角三角形两锐角互余的性质，是基础题，熟记性质是解题的关键．
练习册系列答案
相关题目
3．如果下列各组数是三角形的三边长，那么不能组成直角三角形的一组数是（ ）
| A． | 1，$\sqrt{3}$，2 | B． | 2，3，4 | C． | 5，13，12 | D． | $\frac{3}{5}$，$\frac{4}{5}$，1 |
4．
如图，已知AB∥CD∥EF，则x、y、z三者之间的关系是（ ）
如图，已知AB∥CD∥EF，则x、y、z三者之间的关系是（ ）| A． | x+y+z=180° | B． | x+y-z=180° | C． | y-x-z=0° | D． | y-x-2z=0° |
1．
菱形ABCD的两条对角线相交于O，若AC=6，BD=8，则菱形ABCD的周长是（ ）
菱形ABCD的两条对角线相交于O，若AC=6，BD=8，则菱形ABCD的周长是（ ）| A． | $4\sqrt{3}$ | B． | 20 | C． | 24 | D． | $2\sqrt{3}$ |
8．
如图，△ABC≌△ADE，若∠B=80°，∠C=30°，∠DAB：∠DAC=4：3，则∠EFC的度数为（ ）
如图，△ABC≌△ADE，若∠B=80°，∠C=30°，∠DAB：∠DAC=4：3，则∠EFC的度数为（ ）| A． | 30° | B． | 40° | C． | 70° | D． | 80° |
18．
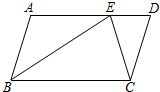如图，在?ABCD中，AB=6，BC=10，E为AD上一点，且BE=BC，CE=CD，则DE等于（ ）
如图，在?ABCD中，AB=6，BC=10，E为AD上一点，且BE=BC，CE=CD，则DE等于（ ）| A． | 5 | B． | 4 | C． | 3.6 | D． | 3 |
5．
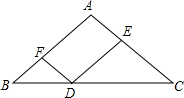如图，在△ABC中，AB=AC=8，点D在BC上，DE∥AB，DF∥AC，则四边形AFDE的周长是（ ）
如图，在△ABC中，AB=AC=8，点D在BC上，DE∥AB，DF∥AC，则四边形AFDE的周长是（ ）| A． | 24 | B． | 18 | C． | 16 | D． | 12 |
2．在-2，+3.5，0，$\frac{2}{3}$，-0.7，11中，负数有（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
3．
如图是某班50名同学爱心捐款额的频数分布直方图（每组含前一个边界值，不含后一个边界值），则捐款人数最多的一组是（ ）
如图是某班50名同学爱心捐款额的频数分布直方图（每组含前一个边界值，不含后一个边界值），则捐款人数最多的一组是（ ）| A． | 5-10元 | B． | 10-15元 | C． | 15-20元 | D． | 20-25元 |