题目内容
7.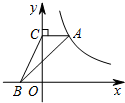 如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}$(x>0)的图象上,过点A作AC⊥y轴于点C,点B在x轴上,连结CB、AB.若△ABC的面积为4,则k的值为8.
如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}$(x>0)的图象上,过点A作AC⊥y轴于点C,点B在x轴上,连结CB、AB.若△ABC的面积为4,则k的值为8.
分析 连接OA,由△ABC和△OAC的面积相等可得出关于k的一元一次方程,解方程即可得出结论.
解答 解:连接OA,如图所示.
∵△ABC和△OAC的面积相等(同底等高),
∴S△OAC=$\frac{1}{2}$k=4,
∴k=8.
故答案为8.
点评 本题考查了反比例函数系数k的几何意义,解题的关键是找出S△OAC=$\frac{1}{2}$k=4.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数系数k的几何意义找出相对应的三角形的面积是关键.

练习册系列答案
相关题目
17.下列计算正确的是( )
| A. | (a2)3=a5 | B. | a2•a=a3 | C. | a6÷a3=a2 | D. | (ab)2=ab2 |
18.-(-2)的相反数是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | -$\frac{1}{2}$ |
12.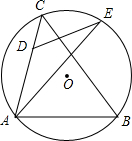 如图,△ABC内接于圆O,点D在AC边上,AD=2CD,在BC弧上取一点E,使得∠CDE=∠ABC,连接AE,则$\frac{AE}{DE}$等于( )
如图,△ABC内接于圆O,点D在AC边上,AD=2CD,在BC弧上取一点E,使得∠CDE=∠ABC,连接AE,则$\frac{AE}{DE}$等于( )
 如图,△ABC内接于圆O,点D在AC边上,AD=2CD,在BC弧上取一点E,使得∠CDE=∠ABC,连接AE,则$\frac{AE}{DE}$等于( )
如图,△ABC内接于圆O,点D在AC边上,AD=2CD,在BC弧上取一点E,使得∠CDE=∠ABC,连接AE,则$\frac{AE}{DE}$等于( )| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
16.若x,y都是有理数,且|4-3x+y|与(3-4x-y)2互为相反数,则x,y的值分别为( )
| A. | x=-1,y=2 | B. | x=1,y=-1 | C. | x=0,y=-$\frac{3}{5}$ | D. | x=3,y=1 |
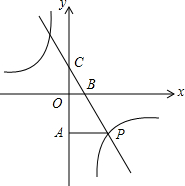 如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y=$\frac{n}{x}$的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,-6),且S△CAP=18.
如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y=$\frac{n}{x}$的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,-6),且S△CAP=18.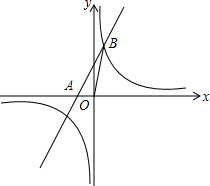 如图,直线y=2x+3与反比例函数y=$\frac{k}{x}$的图象相交于点B(a,5),且与x轴相交于点A.
如图,直线y=2x+3与反比例函数y=$\frac{k}{x}$的图象相交于点B(a,5),且与x轴相交于点A.