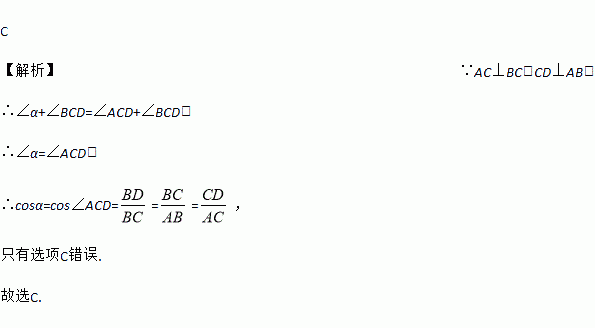题目内容
如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
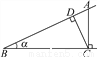
A. 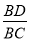 B.
B. 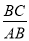 C.
C. 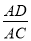 D.
D. 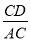
 C
【解析】∵AC⊥BC,CD⊥AB,
∴∠α+∠BCD=∠ACD+∠BCD,
∴∠α=∠ACD,
∴cosα=cos∠ACD===,
只有选项C错误.
故选C.
C
【解析】∵AC⊥BC,CD⊥AB,
∴∠α+∠BCD=∠ACD+∠BCD,
∴∠α=∠ACD,
∴cosα=cos∠ACD===,
只有选项C错误.
故选C.
练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
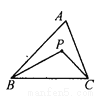
已知:如图,P是△ABC内任一点,求证:∠BPC>∠A.
 说明见解析.
【解析】试题分析:延长BP交AC于D. 根据△PDC外角的性质知∠BPC>∠PDC,根据△ABD外角的性质知∠PDC>∠A,所以易证∠BPC>∠A.
试题解析:如图,延长BP交AC于D.
∵∠BPC>∠PDC,∠PDC>∠A,
∴∠BPC>∠A.
说明见解析.
【解析】试题分析:延长BP交AC于D. 根据△PDC外角的性质知∠BPC>∠PDC,根据△ABD外角的性质知∠PDC>∠A,所以易证∠BPC>∠A.
试题解析:如图,延长BP交AC于D.
∵∠BPC>∠PDC,∠PDC>∠A,
∴∠BPC>∠A. 已知分式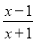 的值是零,那么x的值是( )
的值是零,那么x的值是( )
A. -1 B. 0
C. 1 D. ±1
 C
【解析】由题意得:x-1=0,则x=1,故选C.
C
【解析】由题意得:x-1=0,则x=1,故选C. 如图,为了测量电线杆AB的高度,小明将测量仪放在与电线杆的水平距离为9m的D处.若测角仪CD的高度为1.5m,在C处测得电线杆顶端A的仰角为36°,则电线杆AB的高度约为____(精确到0.1m).(参考数据sin36°≈0.59.cos36°≈0.81,tan36°≈0.73).
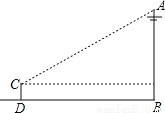
 8.1 m.
【解析】如图作CE⊥AB,垂足为E.
∵=tan 36°,
CE=BD,
∴AE=BD·tan 36°
≈9×0.73
=6.57,
∴AB=6.57+1.5=8.07≈8.1.
8.1 m.
【解析】如图作CE⊥AB,垂足为E.
∵=tan 36°,
CE=BD,
∴AE=BD·tan 36°
≈9×0.73
=6.57,
∴AB=6.57+1.5=8.07≈8.1. 在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosA=( )
A. 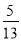 B.
B. 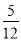 C.
C. 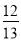 D.
D. 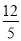
 C
【解析】∵Rt△ABC中,∠C=90°,AB=13,AC=12,
∴cosA= = .
故选:C.
C
【解析】∵Rt△ABC中,∠C=90°,AB=13,AC=12,
∴cosA= = .
故选:C. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的正弦值为 .
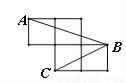
 【解析】
试题分析:本题首先将∠ABC转化到某一个直角三角形中,然后进行求值.
【解析】
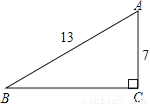
试题分析:本题首先将∠ABC转化到某一个直角三角形中,然后进行求值. 如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB= .
 .
【解析】试题分析:根据锐角三角函数定义直接进行解答.
【解析】
∵在Rt△ABC中,∠C=90°,AB=13,AC=7,
∴sinB==.
故答案为:.
.
【解析】试题分析:根据锐角三角函数定义直接进行解答.
【解析】
∵在Rt△ABC中,∠C=90°,AB=13,AC=7,
∴sinB==.
故答案为:. 小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).
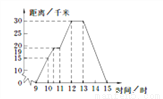
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
 (1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)11千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
【解析】解:(1)图象表示了时间、距离的关系,自变量是时间,因变量是距离. (2)由图象看出10时他距家15千米,13时他距家30千米. (3)由图象看...
(1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)11千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
【解析】解:(1)图象表示了时间、距离的关系,自变量是时间,因变量是距离. (2)由图象看出10时他距家15千米,13时他距家30千米. (3)由图象看... 如图,在△ABC中,AB=AC,CD平分∠ACB,∠A=36°,则∠BDC的度数为 .
 72
【解析】由AB=AC,CD平分∠ACB,∠A=36°,根据三角形内角和180°可求得∠B等于∠ACB,并能求出其角度,在△DBC求得所求角度.
【解析】
∵AB=AC,CD平分∠ACB,∠A=36°,
∴∠B=(180°-36°)÷2=72°,∠DCB=36°.
∴∠BDC=72°.
故答案为:72°
72
【解析】由AB=AC,CD平分∠ACB,∠A=36°,根据三角形内角和180°可求得∠B等于∠ACB,并能求出其角度,在△DBC求得所求角度.
【解析】
∵AB=AC,CD平分∠ACB,∠A=36°,
∴∠B=(180°-36°)÷2=72°,∠DCB=36°.
∴∠BDC=72°.
故答案为:72°