题目内容
如图，已知∠ABC=∠DCB，下列所给条件不能证明△ABC≌△DCB的是( )
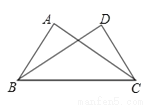
A. ∠A=∠D B. AB=DC C. ∠ACB=∠DBC D. AC=BD
D
【解析】试题分析：根据题目所给条件∠ABC=∠DCB，再加上公共边BC=BC，然后再结合判定定理分别进行分析即可．
【解析】
A、添加∠A=∠D可利用AAS判定△ABC≌△DCB，故此选项不合题意；
B、添加AB=DC可利用SAS定理判定△ABC≌△DCB，故此选项不合题意；
C、添加∠ACB=∠DBC可利用ASA定理判定△ABC≌△DCB，故此选项不合题意；
...
练习册系列答案
相关题目
如图，在Rt△ABC中，∠C=90°，AB=13，AC=7，则sinB= ．
．
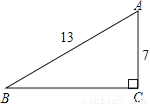
【解析】试题分析：根据锐角三角函数定义直接进行解答．
【解析】
∵在Rt△ABC中，∠C=90°，AB=13，AC=7，
∴sinB==．
故答案为：． 如图所示，一个能张开54°的圆规，若两脚长均为15 cm，则该圆规所画的圆中最大的直径是多少?(sin 27°≈0.4540，精确到0.01 cm)
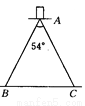
27.24cm
【解析】试题分析：作AD⊥BC于D，根据等腰三角形的性质求出BD的长，即可求出BC的长.
试题解析：作AD⊥BC于D，则∠BAD=27°，
∴BD=ABsin 27°=15×sin 27°≈15×0.4540=6.81(cm)，∴BC=2BD≈2×6.81=13.62(cm)，∴直径=2BC≈2×13.62=27.24(cm)．即该圆规所画的圆中最大的直径约是27... 如图，在△ABC中，AB=AC，CD平分∠ACB，∠A=36°，则∠BDC的度数为 .
72
【解析】由AB=AC，CD平分∠ACB，∠A=36°，根据三角形内角和180°可求得∠B等于∠ACB，并能求出其角度，在△DBC求得所求角度．
【解析】
∵AB=AC，CD平分∠ACB，∠A=36°，
∴∠B=（180°-36°）÷2=72°，∠DCB=36°．
∴∠BDC=72°．
故答案为：72° 如图，△ABC中，AB=AC,∠B=70°，则∠A的度数是（ ）
A. 70° B. 55° C. 50° D. 40°
D
【解析】试题解析：【解析】
∵AB＝AC，
∴∠B＝∠C，
∵∠B＝70°，
∴∠C＝70°，
∵∠A＋∠B＋∠C＝180°，
∴∠A＝40°.
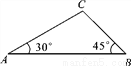
故应选D. 如图，在△ABC中，∠A＝30°，∠B＝45°，AC＝2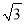
，则AB的长为_______．
3＋
【解析】过C作CD⊥AB于D，∴∠ADC＝∠BDC＝90°．∵∠B＝45°，∴∠BCD＝∠B＝45°，
∴CD＝BD．∵∠A＝30°，，∴，∴．
由勾股定理得： ，∴． 在一个不透明的袋子中装有仅颜色不同的10个小球，其中红球4个，黑球6个．
(1)先从袋子中取出m(m>1)个红球，再从袋子中随机摸出1个球，将“摸出黑球”记为事件A．请完成下列表格：
事件A | 必然事件 | 随机事件 |
m的值 |
(2)先从袋子中取出m个红球，再放入m个一样的黑球并摇匀，随机摸出1个球是黑球的可能性大小是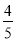
，求m的值．
(1)填表见解析；（2）2.
【解析】试题分析：（1）当袋子中全部为黑球时，摸出黑球才是必然事件，否则就是随机事件；
（2）利用概率公式列出方程，求得m的值即可．
试题解析：（1）当袋子中全为黑球，即摸出4个红球时，摸到黑球是必然事件；
当摸出2个或3个时，摸到黑球为随机事件，
故答案为：4；2，3.
（2）根据题意得： ，
解得：m=2，
所以m的... 用力转动如图所示的转盘甲和转盘乙的指针,如果想让指针停在阴影区域,选取哪个转盘成功的机会比较大?( )
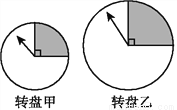
A. 转盘甲 B. 转盘乙 C. 两个一样大 D. 无法确定
C
【解析】【解析】
虽然两圆面积不同，但是阴影部分均占，故指针指向黑色部分的概率相同．故选C． 不一定在三角形内部的线段是( )
A. 三角形的角平分线 B. 三角形的中线
C. 三角形的高 D. 以上都不对
C
【解析】试题解析：三角形的角平分线、中线一定在三角形的内部，
直角三角形的高线有两条是三角形的直角边，
钝角三角形的高线有两条在三角形的外部，
所以，不一定在三角形内部的线段是三角形的高.
故选C.