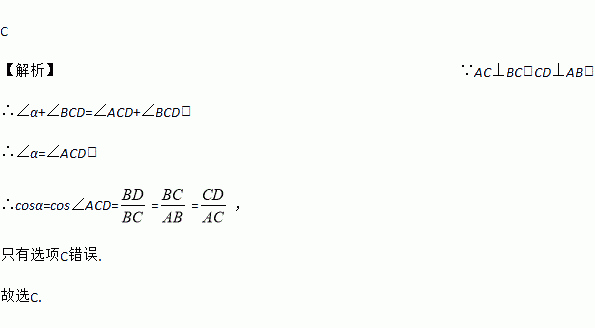题目内容
如图,点A为∠α边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
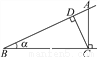
A. 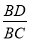 B.
B. 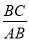 C.
C. 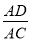 D.
D. 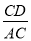
 C
【解析】∵AC⊥BC,CD⊥AB,
∴∠α+∠BCD=∠ACD+∠BCD,
∴∠α=∠ACD,
∴cosα=cos∠ACD===,
只有选项C错误.
故选C.
C
【解析】∵AC⊥BC,CD⊥AB,
∴∠α+∠BCD=∠ACD+∠BCD,
∴∠α=∠ACD,
∴cosα=cos∠ACD===,
只有选项C错误.
故选C.
能将一个三角形分成面积相等的两个三角形的一条线段是 ( )
A. 中线 B. 角平分线 C. 高线 D. 三角形的角平分线
 A
【解析】试题解析:∵三角形的中线把三角形分成的两个三角形,底边相等,高是同一条高,
∴分成的两三角形的面积相等.
故选A.
A
【解析】试题解析:∵三角形的中线把三角形分成的两个三角形,底边相等,高是同一条高,
∴分成的两三角形的面积相等.
故选A. 在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosA=( )
A. 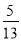 B.
B. 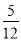 C.
C. 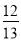 D.
D. 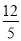
 C
【解析】∵Rt△ABC中,∠C=90°,AB=13,AC=12,
∴cosA= = .
故选:C.
C
【解析】∵Rt△ABC中,∠C=90°,AB=13,AC=12,
∴cosA= = .
故选:C. 如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB= .
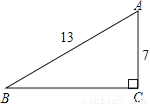
 .
【解析】试题分析:根据锐角三角函数定义直接进行解答.
【解析】
∵在Rt△ABC中,∠C=90°,AB=13,AC=7,
∴sinB==.
故答案为:.
.
【解析】试题分析:根据锐角三角函数定义直接进行解答.
【解析】
∵在Rt△ABC中,∠C=90°,AB=13,AC=7,
∴sinB==.
故答案为:. 在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosA=( )
A. 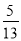 B.
B. 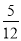 C.
C. 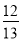 D.
D. 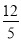
 C
【解析】∵Rt△ABC中,∠C=90°,AB=13,AC=12,
∴cosA= = .
故选:C.
C
【解析】∵Rt△ABC中,∠C=90°,AB=13,AC=12,
∴cosA= = .
故选:C. 小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).
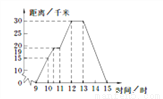
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
 (1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)11千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
【解析】解:(1)图象表示了时间、距离的关系,自变量是时间,因变量是距离. (2)由图象看出10时他距家15千米,13时他距家30千米. (3)由图象看...
(1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)11千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
【解析】解:(1)图象表示了时间、距离的关系,自变量是时间,因变量是距离. (2)由图象看出10时他距家15千米,13时他距家30千米. (3)由图象看... 某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:

设鸭的质量为x千克,烤制时间为t,估计当x=3.2千克时,t的值为( )
A. 140 B. 138 C. 148 D. 160
 C
【解析】从表中可以看出,烤鸭的质量每增加0.5千克,烤制的时间增加20分钟,由此可以知道烤制时间是烤鸭质量的一次函数.
设烤制时间为t分钟,烤鸭的质量为x千克t与x的一次函数关系式为:,
,
计算得出
所以.
当千克时,.
故选C.
C
【解析】从表中可以看出,烤鸭的质量每增加0.5千克,烤制的时间增加20分钟,由此可以知道烤制时间是烤鸭质量的一次函数.
设烤制时间为t分钟,烤鸭的质量为x千克t与x的一次函数关系式为:,
,
计算得出
所以.
当千克时,.
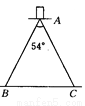
故选C. 如图所示,一个能张开54°的圆规,若两脚长均为15 cm,则该圆规所画的圆中最大的直径是多少?(sin 27°≈0.4540,精确到0.01 cm)
 27.24cm
【解析】试题分析:作AD⊥BC于D,根据等腰三角形的性质求出BD的长,即可求出BC的长.
试题解析:作AD⊥BC于D,则∠BAD=27°,
∴BD=ABsin 27°=15×sin 27°≈15×0.4540=6.81(cm),∴BC=2BD≈2×6.81=13.62(cm),∴直径=2BC≈2×13.62=27.24(cm).即该圆规所画的圆中最大的直径约是27...
27.24cm
【解析】试题分析:作AD⊥BC于D,根据等腰三角形的性质求出BD的长,即可求出BC的长.
试题解析:作AD⊥BC于D,则∠BAD=27°,
∴BD=ABsin 27°=15×sin 27°≈15×0.4540=6.81(cm),∴BC=2BD≈2×6.81=13.62(cm),∴直径=2BC≈2×13.62=27.24(cm).即该圆规所画的圆中最大的直径约是27... 在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A | 必然事件 | 随机事件 |
m的值 |
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的可能性大小是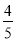 ,求m的值.
,求m的值.
 (1)填表见解析;(2)2.
【解析】试题分析:(1)当袋子中全部为黑球时,摸出黑球才是必然事件,否则就是随机事件;
(2)利用概率公式列出方程,求得m的值即可.
试题解析:(1)当袋子中全为黑球,即摸出4个红球时,摸到黑球是必然事件;
当摸出2个或3个时,摸到黑球为随机事件,
故答案为:4;2,3.
(2)根据题意得: ,
解得:m=2,
所以m的...
(1)填表见解析;(2)2.
【解析】试题分析:(1)当袋子中全部为黑球时,摸出黑球才是必然事件,否则就是随机事件;
(2)利用概率公式列出方程,求得m的值即可.
试题解析:(1)当袋子中全为黑球,即摸出4个红球时,摸到黑球是必然事件;
当摸出2个或3个时,摸到黑球为随机事件,
故答案为:4;2,3.
(2)根据题意得: ,
解得:m=2,
所以m的...