题目内容
用一张正方形的红纸沿对角线对折后,得到一个等腰直角三角形,再沿斜边上的高对折,得到的又是等腰直角三角形,在此三角形上剪出一些花纹,然后打开折叠的纸,将它铺平,小明一下子就猜出了这个图案至少有( )条对称轴.
A. 0 B. 2 C. 4 D. 6
 B
【解析】根据轴对称的性质或动手操作即可得出答案.
【解析】
对折线有两条,而没展开的花纹不一定是轴对称,所以至少有2条对称轴.
故选B.
B
【解析】根据轴对称的性质或动手操作即可得出答案.
【解析】
对折线有两条,而没展开的花纹不一定是轴对称,所以至少有2条对称轴.
故选B.
练习册系列答案
相关题目
已知点A(2m,-3)与B(6,1-n)关于原点对称,求出m和n的值.
 m=-3,n=-2.
【解析】试题分析:根据点关于原点对称的特征, 关于原点的对称点,横纵坐标都变成相反数,可得:2m+6=0,-3+1-n=0,解得: m=-3,n=-2.
试题解析:因为点A,B关于原点对称,所以,解得m=-3,n=-2.
m=-3,n=-2.
【解析】试题分析:根据点关于原点对称的特征, 关于原点的对称点,横纵坐标都变成相反数,可得:2m+6=0,-3+1-n=0,解得: m=-3,n=-2.
试题解析:因为点A,B关于原点对称,所以,解得m=-3,n=-2. 能将一个三角形分成面积相等的两个三角形的一条线段是 ( )
A. 中线 B. 角平分线 C. 高线 D. 三角形的角平分线
 A
【解析】试题解析:∵三角形的中线把三角形分成的两个三角形,底边相等,高是同一条高,
∴分成的两三角形的面积相等.
故选A.
A
【解析】试题解析:∵三角形的中线把三角形分成的两个三角形,底边相等,高是同一条高,
∴分成的两三角形的面积相等.
故选A. 已知分式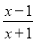 的值是零,那么x的值是( )
的值是零,那么x的值是( )
A. -1 B. 0
C. 1 D. ±1
 C
【解析】由题意得:x-1=0,则x=1,故选C.
C
【解析】由题意得:x-1=0,则x=1,故选C. 以给出的图形“○○,△△, ”(两个圆、两个三角形、两条平行线)为构件,设计一个构思独特且有意义的轴对称图形.举例:如图①是符合要求的一个图形,你还能构思出其他的图形吗?请在图②中画出与之不同的一个图形,并写出一两句贴切的解说词.
”(两个圆、两个三角形、两条平行线)为构件,设计一个构思独特且有意义的轴对称图形.举例:如图①是符合要求的一个图形,你还能构思出其他的图形吗?请在图②中画出与之不同的一个图形,并写出一两句贴切的解说词.
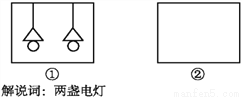
 能;
【解析】利用轴对称进行设计图案即可.
【解析】
如图所示.
解说词:两人相伴.
能;
【解析】利用轴对称进行设计图案即可.
【解析】
如图所示.
解说词:两人相伴. 如图,为了测量电线杆AB的高度,小明将测量仪放在与电线杆的水平距离为9m的D处.若测角仪CD的高度为1.5m,在C处测得电线杆顶端A的仰角为36°,则电线杆AB的高度约为____(精确到0.1m).(参考数据sin36°≈0.59.cos36°≈0.81,tan36°≈0.73).
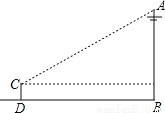
 8.1 m.
【解析】如图作CE⊥AB,垂足为E.
∵=tan 36°,
CE=BD,
∴AE=BD·tan 36°
≈9×0.73
=6.57,
∴AB=6.57+1.5=8.07≈8.1.
8.1 m.
【解析】如图作CE⊥AB,垂足为E.
∵=tan 36°,
CE=BD,
∴AE=BD·tan 36°
≈9×0.73
=6.57,
∴AB=6.57+1.5=8.07≈8.1. 在Rt△ABC中,∠C=90°,AB=13,AC=12,则cosA=( )
A. 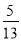 B.
B. 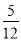 C.
C. 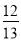 D.
D. 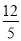
 C
【解析】∵Rt△ABC中,∠C=90°,AB=13,AC=12,
∴cosA= = .
故选:C.
C
【解析】∵Rt△ABC中,∠C=90°,AB=13,AC=12,
∴cosA= = .
故选:C. 如图,在Rt△ABC中,∠C=90°,AB=13,AC=7,则sinB= .
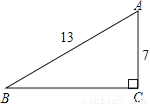
 .
【解析】试题分析:根据锐角三角函数定义直接进行解答.
【解析】
∵在Rt△ABC中,∠C=90°,AB=13,AC=7,
∴sinB==.
故答案为:.
.
【解析】试题分析:根据锐角三角函数定义直接进行解答.
【解析】
∵在Rt△ABC中,∠C=90°,AB=13,AC=7,
∴sinB==.
故答案为:. 如图所示,一个能张开54°的圆规,若两脚长均为15 cm,则该圆规所画的圆中最大的直径是多少?(sin 27°≈0.4540,精确到0.01 cm)
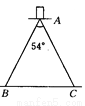
 27.24cm
【解析】试题分析:作AD⊥BC于D,根据等腰三角形的性质求出BD的长,即可求出BC的长.
试题解析:作AD⊥BC于D,则∠BAD=27°,
∴BD=ABsin 27°=15×sin 27°≈15×0.4540=6.81(cm),∴BC=2BD≈2×6.81=13.62(cm),∴直径=2BC≈2×13.62=27.24(cm).即该圆规所画的圆中最大的直径约是27...
27.24cm
【解析】试题分析:作AD⊥BC于D,根据等腰三角形的性质求出BD的长,即可求出BC的长.
试题解析:作AD⊥BC于D,则∠BAD=27°,
∴BD=ABsin 27°=15×sin 27°≈15×0.4540=6.81(cm),∴BC=2BD≈2×6.81=13.62(cm),∴直径=2BC≈2×13.62=27.24(cm).即该圆规所画的圆中最大的直径约是27... 
