题目内容
13.如图,已知AB是⊙O的直径,过点A作⊙O的切线MA,P为直线MA上一动点,以点P为圆心,PA为半径作⊙P,交⊙O于点C,连接PC、OP、BC.(1)知识探究(如图1):
①判断直线PC与⊙O的位置关系,请证明你的结论;
②判断直线OP与BC的位置关系,请证明你的结论.
(2)知识运用(如图2):
当PA>OA时,直线PC交AB的延长线于点D,若BD=2AB,求tan∠ABC的值.
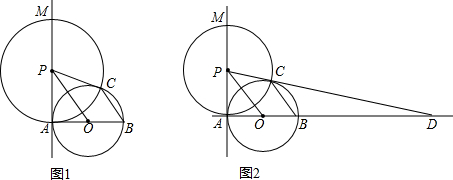
分析 (1)①PC与⊙O相切.易证明△PAO≌△PCO,则∠PAO=∠PCO,由PA是⊙O的切线,可知∠PAO=∠PCO=90°,即可证明结论;
②OP∥BC.由(1)可知∠POA=∠POC,根据同弧所对圆周角是圆心角的一半可知∠ABC=$\frac{1}{2}$∠AOC,根据同位角相等可证明OP∥BC.
(2)根据OP∥BC,可知$\frac{BD}{OD}=\frac{CD}{PD}$,由BD=2AB,可知AD=6OA,OD=5OB,所以PD=5PC,设设PA=PC=R,OA=r,根据勾股定理列方程求出R与r的数量关系,即可在Rt△PAO中求出tan∠ABC=tan∠POA.
解答 (1)①PC与⊙O相切.
证明:如图1,连接OC,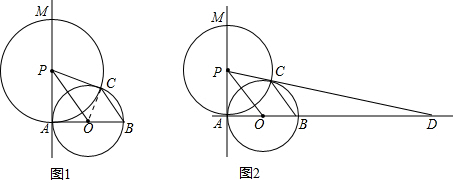 在△PAO和△PCO中,
在△PAO和△PCO中,
$\left\{\begin{array}{l}{OA=OC}\\{PO=PO}\\{PA=PC}\end{array}\right.$,
∴△PAO≌△PCO,
∴∠PAO=∠PCO,
∵PA是⊙O的切线,AB是⊙O的直径,
∴∠PAO=∠PCO=90°,
∴PC与⊙O相切.
②OP∥BC.
证明:∵△PAO≌△PCO,
∴∠POA=∠POC,
又∵∠ABC=$\frac{1}{2}$∠AOC(同弧所对圆周角是圆心角的一半),
∴∠ABC=∠POA,
∴OP∥BC.
(2)解:如图2,
∵BD=2AB,
∴BD=4OB,AD=6OA,
∴$\frac{BD}{OD}=\frac{4}{5}$,
∵OP∥BC,
∴$\frac{BD}{OD}=\frac{CD}{PD}=\frac{4}{5}$,
∴PD=5PC,
设PA=PC=R,OA=r,
∴AD=6r,PD=5R,
∵PA2+AD2=PD2,
∴R2+(6r)2=(5R)2
解得:R=$\frac{\sqrt{6}}{2}$r,
∵tan∠ABC=tan∠POA=$\frac{PA}{OA}$,
∴tan∠ABC═$\frac{PA}{OA}$=$\frac{\frac{\sqrt{6}}{2}r}{r}$=$\frac{\sqrt{6}}{2}$.
点评 本题主要考查了圆的有关性质、切线的性质与判定、平行线分线段成比例定理、勾股定理以及锐角三角函数的综合应用,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

| A. | b=-3 | B. | b=-2 | C. | b=-1 | D. | b=2 |
| A. | $\sqrt{27}$ | B. | $\sqrt{\frac{1}{5}}$ | C. | $\sqrt{16}$ | D. | $\sqrt{10}$ |
| A. | $\sqrt{7}$ | B. | 8 | C. | 9 | D. | 10 |
| 类别 | 频数 | 频率 |
| 助人为乐美德少年 | a | 0.20 |
| 自强自立美德少年 | 3 | b |
| 孝老爱亲美德少年 | 7 | 0.35 |
| 诚实守信美德少年 | 6 | 0.32 |
(1)统计表中的a=4,b0.15;
(2)统计表后两行错误的数据是0.32,该数据的正确值是0.30;
(3)校园小记者决定从A,B,C三位“自强自立美德少年”中随机采访两位,用画树状图或列表的方法,求A,B都被采访到的概率.
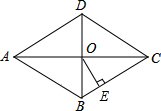 如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE=$\frac{12}{5}$.
如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE=$\frac{12}{5}$. 某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量的$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.
某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量的$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.