题目内容
18.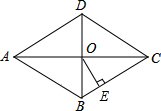 如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE=$\frac{12}{5}$.
如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE=$\frac{12}{5}$.
分析 先根据菱形的性质得AC⊥BD,OB=OD=$\frac{1}{2}$BD=3,OA=OC=$\frac{1}{2}$AC=4,再在Rt△OBC中利用勾股定理计算出BC=5,然后利用面积法计算OE的长.
解答 解:∵四边形ABCD为菱形,
∴AC⊥BD,OB=OD=$\frac{1}{2}$BD=3,OA=OC=$\frac{1}{2}$AC=4,
在Rt△OBC中,∵OB=3,OC=4,
∴BC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵OE⊥BC,
∴$\frac{1}{2}$OE•BC=$\frac{1}{2}$OB•OC,
∴OE=$\frac{3×4}{5}$=$\frac{12}{5}$.
故答案为$\frac{12}{5}$.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.也考查了勾股定理和三角形面积公式.

练习册系列答案
相关题目
6.化简$\sqrt{36×144}$,正确的结果是( )
| A. | ±72 | B. | 72 | C. | 432 | D. | 以上答案都不是 |
7.下列函数是一次函数的是( )
| A. | y=-8x | B. | y=-$\frac{8}{x}$ | C. | y=-8x2+2 | D. | y=-$\frac{8}{x}$+2 |
 如图,正五边形ABCDE内接于⊙O,则∠CAD=36度.
如图,正五边形ABCDE内接于⊙O,则∠CAD=36度. 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )