题目内容
8．在平面直角坐标系中，已知点P的坐标是（6，8），则OP的长为（ ）| A． | $\sqrt{7}$ | B． | 8 | C． | 9 | D． | 10 |
分析 直接根据勾股定理计算即可．
解答 解：∵P（6，8），点O为坐标原点，
∴OP=$\sqrt{{6}^{2}+{8}^{2}}$=10．
答：线段OP的长度为10．
故选D．
点评 本题考查了勾股定理的运用，在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
练习册系列答案
相关题目
16．下列二元一次方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$的是（ ）
| A． | $\left\{\begin{array}{l}{x+y=0}\\{x-y=1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=0}\\{x-y=-1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x+y=0}\\{x-y=2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=0}\\{x-y=-2}\end{array}\right.$ |
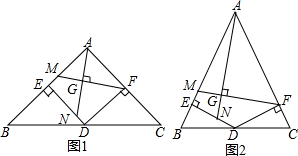
20．
如图，在△ABC中，∠ACB=90°，分别以点A和B为圆心，以相同的长（大于$\frac{1}{2}$AB）为半径作弧，两弧相交于点M和N，作直线MN交AB于点D，交BC于点E，连接CD，下列结论不一定正确的是（ ）
如图，在△ABC中，∠ACB=90°，分别以点A和B为圆心，以相同的长（大于$\frac{1}{2}$AB）为半径作弧，两弧相交于点M和N，作直线MN交AB于点D，交BC于点E，连接CD，下列结论不一定正确的是（ ）| A． | AD=BD | B． | BD=CD | C． | ∠A=∠BED | D． | ∠ECD=∠EDC |
17．
如图，点P是∠AOB内任意一点，OP=5cm，点M和点N分别是射线OA和射线OB上的动点，△PMN周长的最小值是5cm，则∠AOB的度数是（ ）
如图，点P是∠AOB内任意一点，OP=5cm，点M和点N分别是射线OA和射线OB上的动点，△PMN周长的最小值是5cm，则∠AOB的度数是（ ）| A． | 25° | B． | 30° | C． | 35° | D． | 40° |
18．下列正多边形中，不能够铺满地面的是（ ）
| A． | 正五边形 | B． | 正方形 | C． | 正六边形 | D． | 正三角形 |