题目内容
3.已知点A在数轴上对应的数为a,点B对应的数为b,且|a+4|+(b-3)2=0.(1)则a=-4,b=3;并将这两数在数轴上所对应的点A、B表示出来;
(2)数轴上在B点右边有一点C到A、B两点的距离和为11,求点C的数轴上所对应的数;
(3)若A点,B点同时沿数轴向正方向运动,点A的速度是点B的2倍,且3秒后,2OA=OB,求点B的速度.
友情提示:M、N之间距离记作|MN|,点M、N在数轴上对应的数分别为m、n,则|MN|=|m-n|.

分析 (1)利用绝对值的非负性质得到a+4=0,b-3=0,解得a=-4,b=3;
(2)设点C在数轴上所对应的数为x,根据CA+CB=11列出方程,解方程即可;
(3)设点B的速度为v,则A的速度为2v,分A在原点O的左边与A在原点O的右边进行讨论.
解答 解:(1)∵且|a+4|+(b-3)2=0.
∴a+4=0,b-3=0,
解得a=-4,b=3.
点A、B表示在数轴上为: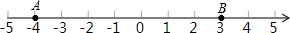
故答案是:-4;3;
(2)设点C在数轴上所对应的数为x,
∵C在B点右边,
∴x>3.
根据题意得
x-3+x-(-4)=11,
解得x=5.
即点C在数轴上所对应的数为5;
(3)设B速度为v,则A的速度为2v,
3秒后点,A点在数轴上表示的数为(-4+6v),B点在数轴上表示的数为3+3v,
当A还在原点O的左边时,由2OA=OB可得-2(-4+6v)=3+3v,解得v=$\frac{1}{3}$;
当A在原点O的右边时,由2OA=OB可得2(-4+6v)=3+3v,解得v=$\frac{11}{9}$.
即点B的速度为$\frac{1}{3}$或$\frac{11}{9}$.
点评 本题考查了一元一次方程的应用与数轴,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
13. 如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是( )°.(用含x的式子表示)
如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是( )°.(用含x的式子表示)
 如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是( )°.(用含x的式子表示)
如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是( )°.(用含x的式子表示)| A. | x | B. | 180°-2x | C. | 180°-x | D. | 2x |
14. 有理数a、b在数轴上的位置如图,则化简式子|a+b|-a的结果是( )
有理数a、b在数轴上的位置如图,则化简式子|a+b|-a的结果是( )
 有理数a、b在数轴上的位置如图,则化简式子|a+b|-a的结果是( )
有理数a、b在数轴上的位置如图,则化简式子|a+b|-a的结果是( )| A. | 2a+b | B. | 2a | C. | b | D. | -2a-b |
 要求:在下列空白处尺规作图,保留作图痕迹,不写作法,要作答.
要求:在下列空白处尺规作图,保留作图痕迹,不写作法,要作答. 已知直线l1:y1=2x+3与直线l2:y2=kx-1交于A点,A点横坐标为-1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.
已知直线l1:y1=2x+3与直线l2:y2=kx-1交于A点,A点横坐标为-1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点. 为加强与家长的沟通,某校在家长会到来之前需印刷《致家长的一封信》等材料以作宣传,该校的印刷任务原来由甲复印店承接,其收费y(元)与印刷页数x(页)的函数关系如图所示.
为加强与家长的沟通,某校在家长会到来之前需印刷《致家长的一封信》等材料以作宣传,该校的印刷任务原来由甲复印店承接,其收费y(元)与印刷页数x(页)的函数关系如图所示.