题目内容
18. 已知直线l1:y1=2x+3与直线l2:y2=kx-1交于A点,A点横坐标为-1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.
已知直线l1:y1=2x+3与直线l2:y2=kx-1交于A点,A点横坐标为-1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.(1)求出A、B、C、D点坐标;
(2)求出直线l2的解析式;
(2)连结BC,求出S△ABC.
分析 (1)把A横坐标代入直线l1解析式求出纵坐标,确定出A坐标,代入直线l2解析式求出k的值,确定出直线l2解析式,即可确定出A、B、C、D坐标;
(2)由k的值确定出直线l2的解析式即可;
(3)求出直线l2与x轴交点E坐标,三角形ABC面积=三角形ABE面积+三角形BCE面积,求出即可.
解答 解:(1)把x=-1代入y1=2x+3,得:y=1,即A(-1,1),
对于y1=2x+3,
令x=0,得到y=3;令y=0,得到x=-1.5,
∴B(-1.5,0),D(0,3),
把A(-1,1)代入y2=kx-1得:k=-2,即y2=-2x-1,
令x=0,得到y=-1,即C(0,-1);
(2)把A(-1,1)代入y2=kx-1得:k=-2,
则y2=-2x-1;
(3)连接BC,设直线l2与x轴交于点E,如图所示,
对于y2=-2x-1,令y=0,得到x=-0.5,即OE=0.5,
∴BE=OB-OE=1.5-0.5=1,
则S△ABC=S△ABE+S△BCE=$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×1=1.
点评 此题考查了两直线相交与平行问题,待定系数法确定一次函数解析式,一次函数与坐标轴的交点,以及三角形面积求法,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
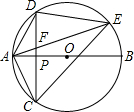 如图,AB是⊙O直径,弦CD⊥AB于P,E是⊙O上一点,连结AD、AC、AE、DE、CE.
如图,AB是⊙O直径,弦CD⊥AB于P,E是⊙O上一点,连结AD、AC、AE、DE、CE.
 如图,按要求画图:
如图,按要求画图: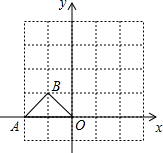 如图,在平面直角坐标系中,△AOB的顶点A(-2,0)、B(-1,1).将△AOB绕点O顺时针旋转90°后,点A、B分别落在A′、B′.
如图,在平面直角坐标系中,△AOB的顶点A(-2,0)、B(-1,1).将△AOB绕点O顺时针旋转90°后,点A、B分别落在A′、B′.