如图.等腰△ABC的周长为21.底边BC=5.AB的垂直平分线DE交AB于点E.交AC于点D.则△BDC的周长为( ) A.13B.14C.15D.12 题目和参考答案——青夏教育精英家教网—

题目内容

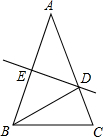如图，等腰△ABC的周长为21，底边BC=5，AB的垂直平分线DE交AB于点E，交AC于点D，则△BDC的周长为（　　）

A、13

B、14

C、15

D、12

考点：线段垂直平分线的性质,等腰三角形的性质

专题：

分析：先根据等腰△ABC的周长为21，底边BC=5得出其腰长，再根据线段垂直平分线的性质即可得出结论．

解答：解：∵等腰△ABC的周长为21，底边BC=5，
∴AB=AC=

21-5

=8．
∵AB的垂直平分线DE交AB于点E，
∴AD=BD，即AD+CD=BD+CD=AC，
∴△BDC的周长=BC+（AD+CD）=BC+AC=5+5=13．
故选A．

点评：本题考查的是线段垂直平分线的性质，熟知垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．

练习册系列答案

相关题目

方程：（1）x³-64=0，（2）3x⁵-96=0，（3）

x³+32=0，（4）x⁴-1=0，（5）2x³-3=0，（6）3x+1=0．这些方程中有

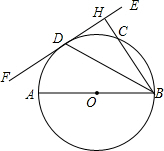如图，AB为⊙O的直径，EF切⊙O于点D，过点B作BH⊥EF于点H，交⊙O于点C，连接BD．
（1）求证：BD平分∠ABH；
（2）如果AB=12，sin∠ABC=

，求DH和BC的长．

将长为a，宽为b（a＞b）的长方形纸片折叠，折痕经过长方形的一个顶点和较长边的中点（如图1），沿折痕剪成一个三角形和一个梯形（如图2）．

（1）利用剪开的两个图形分别拼成一个既无重叠又无空隙的平行四边形、梯形和三角形，分别画出它们对应的图形；
（2）利用若干个剪开的三角形和梯形两种纸片拼成一个无重叠、无缝隙大直角梯形（上、下底分别为a、2a，高为2b），请你在图3中画出拼接线，并保留画图痕迹；
（3）利用5张如图1所示的长方形纸片放在大长方形内（如图4），若左上角与右下角阴影部分的周长相等，求a与b之间的关系式．

某学习小组由3名男生和1名女生组成，如果随机抽取2名同学，求同为男生的概率（请用无序排列组合做）．

圆锥体的底面半径为2，侧面积为8π，则其侧面展开图的圆心角等于

．

下列函数中，当x＞0时，y随x的增大而减小的是（　　）

如图所示，AB∥CD，AC⊥BC，∠BAC=70°，则∠BCD=

试题分类