题目内容
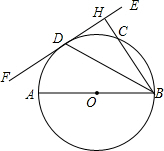 如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.(1)求证:BD平分∠ABH;
(2)如果AB=12,sin∠ABC=
| ||
| 3 |
考点:切线的性质,解直角三角形
专题:证明题
分析:(1)连结OD,如图,根据切线的性质得EF⊥OD,而BH⊥EF,则OD∥BH,利用平行线的性质得∠2=∠3,加上∠1=∠3,所以∠1=∠2;
(2)作OG⊥BC于G,如图,根据垂径定理得BG=CG,在Rt△OBG中,利用正弦的定义可计算出OG=2
,再证明四边形OGHD为矩形得到DE=OG=2
,然后在Rt△OBG中利用勾股定理计算出BG=4,从而得到BC=2BG=8.
(2)作OG⊥BC于G,如图,根据垂径定理得BG=CG,在Rt△OBG中,利用正弦的定义可计算出OG=2
| 5 |
| 5 |
解答: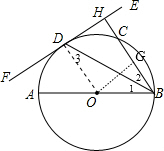 (1)证明:连结OD,如图,
(1)证明:连结OD,如图,
∵EF切⊙O于点D,
∴EF⊥OD,
∵BH⊥EF,
∴OD∥BH,
∴∠2=∠3,
∵OB=OD,
∴∠1=∠3,
∴∠1=∠2,
∴BD平分∠ABH;
(2)解:作OG⊥BC于G,如图,则BG=CG,
在Rt△OBG中,sin∠OBG=
=
,
而OB=6,
∴OG=2
,
∵OD⊥DH,GH⊥DH,
∴四边形OGHD为矩形,
∴DE=OG=2
,
在Rt△OBG中,∵OB=6,OG=2
,
∴BG=
=4,
∴BC=2BG=8.
 (1)证明:连结OD,如图,
(1)证明:连结OD,如图,∵EF切⊙O于点D,
∴EF⊥OD,
∵BH⊥EF,
∴OD∥BH,
∴∠2=∠3,
∵OB=OD,
∴∠1=∠3,
∴∠1=∠2,
∴BD平分∠ABH;
(2)解:作OG⊥BC于G,如图,则BG=CG,
在Rt△OBG中,sin∠OBG=
| OG |
| OB |
| ||
| 3 |
而OB=6,
∴OG=2
| 5 |
∵OD⊥DH,GH⊥DH,
∴四边形OGHD为矩形,
∴DE=OG=2
| 5 |
在Rt△OBG中,∵OB=6,OG=2
| 5 |
∴BG=
| OB2-OG2 |
∴BC=2BG=8.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径;运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了解直角三角形.

练习册系列答案
相关题目
 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°,则∠COE=( )
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°,则∠COE=( )| A、65° | B、70° |
| C、75° | D、80° |
已知锐角α,且sinα=cos37°,则α等于( )
| A、37° | B、63° |
| C、53° | D、45° |
如果收入100元记作+100元,那么支出60元应记作( )元.
| A、-40 | B、+40 |
| C、-60 | D、+60 |
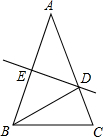 如图,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点E,交AC于点D,则△BDC的周长为( )
如图,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点E,交AC于点D,则△BDC的周长为( )| A、13 | B、14 | C、15 | D、12 |
已知⊙O的直径是10,点P是直径l上的一动点,且点P到点O的最短距离为6,则直线l与⊙O的位置关系是( )
| A、相离 | B、相切 |
| C、相交 | D、无法判断 |