题目内容
 如图,在△ABC中,BC的垂直平分线DE将△ABC的面积分成1:3的两部分.请问E点是否为AB的中点?说明理由.
如图,在△ABC中,BC的垂直平分线DE将△ABC的面积分成1:3的两部分.请问E点是否为AB的中点?说明理由.考点:线段垂直平分线的性质
专题:
分析:根据线段垂直平分线求出△BDE和△CDE的面积相等,根据在△ABC中,BC的垂直平分线DE将△ABC的面积分成1:3的两部分求出△ACE和△BCE的面积相等,根据三角形的面积公式求出即可.
解答:解:E为AB的中点,
理由是:连接CE,过C作CM⊥AB于M,
∵BC的垂直平分线DE,
∴DE⊥BC,BD=DC,
∴△BDE和△CDE的面积相等,
∵在△ABC中,BC的垂直平分线DE将△ABC的面积分成1:3的两部分,
∴△ACE和△BCE的面积相等,
即
×BE×CM
×AE×CM,
∴BE=AE,
即E为AB的中点.

理由是:连接CE,过C作CM⊥AB于M,
∵BC的垂直平分线DE,
∴DE⊥BC,BD=DC,
∴△BDE和△CDE的面积相等,
∵在△ABC中,BC的垂直平分线DE将△ABC的面积分成1:3的两部分,
∴△ACE和△BCE的面积相等,
即
| 1 |
| 2 |
| 1 |
| 2 |
∴BE=AE,
即E为AB的中点.
点评:本题考查了垂直平分线性质和三角形的面积的应用,注意:等底等高的三角形的面积相等.

练习册系列答案
相关题目
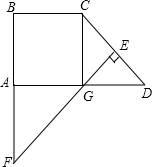 如图所示,直角梯形ABCD中,AD∥BC,∠BAD=90°,∠BCD=135°,CD的垂直平分线交CD于E,交AD于G,交BA延长线于F,AD=4cm.求BF长.
如图所示,直角梯形ABCD中,AD∥BC,∠BAD=90°,∠BCD=135°,CD的垂直平分线交CD于E,交AD于G,交BA延长线于F,AD=4cm.求BF长. 如图,等腰△ABC外一点D,连接DA,DB,DC,且∠ADC=30°.BD=15,AD=12,则CD的长为
如图,等腰△ABC外一点D,连接DA,DB,DC,且∠ADC=30°.BD=15,AD=12,则CD的长为