题目内容
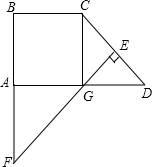 如图所示,直角梯形ABCD中,AD∥BC,∠BAD=90°,∠BCD=135°,CD的垂直平分线交CD于E,交AD于G,交BA延长线于F,AD=4cm.求BF长.
如图所示,直角梯形ABCD中,AD∥BC,∠BAD=90°,∠BCD=135°,CD的垂直平分线交CD于E,交AD于G,交BA延长线于F,AD=4cm.求BF长.考点:直角梯形,线段垂直平分线的性质
专题:
分析:求出DG=CG,根据矩形的性质求出AB=CG=DG,求出AG=AF,推出BF=AD,代入求出即可.
解答:解:连接CG,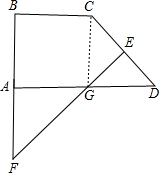
∵EF是CD的垂直平分线,而G在EF上,
∴△CGD为等腰三角形,CG=CD,
∴∠D=∠GCD=45°,
∵BC∥AD,
∴∠DCB=180°-∠D=135°,
∴∠GCB=135°-45°=90°,
∵∠B=90°,
∴平行四边形CBAG是矩形,
∴AB=CG,
∵CG=GD,
∴DG=AB,
∵∠D=45°,
∴∠DGE=∠GED-∠D=90°-45°=45°,
则∠DGE的对角∠FGA=45°
∵∠BAG=90°,
∴∠F=∠BAG-∠FGA=45°=∠FGA,
∴AF=AG,
∴AF+AB=AG+DG,
即BF=AD=4cm.

∵EF是CD的垂直平分线,而G在EF上,
∴△CGD为等腰三角形,CG=CD,
∴∠D=∠GCD=45°,
∵BC∥AD,
∴∠DCB=180°-∠D=135°,
∴∠GCB=135°-45°=90°,
∵∠B=90°,
∴平行四边形CBAG是矩形,
∴AB=CG,
∵CG=GD,
∴DG=AB,
∵∠D=45°,
∴∠DGE=∠GED-∠D=90°-45°=45°,
则∠DGE的对角∠FGA=45°
∵∠BAG=90°,
∴∠F=∠BAG-∠FGA=45°=∠FGA,
∴AF=AG,
∴AF+AB=AG+DG,
即BF=AD=4cm.
点评:本题考查了矩形的 性质和判定,直角梯形的性质,线段垂直平分线性质,等腰三角形的性质的应用,题目比较典型,综合性比较强.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
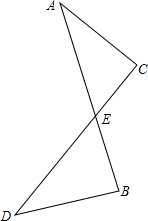 如图,已知AB与CD交于点E,AB与CD的夹角为45°,若∠B+∠C=225°,AC=3,DB=4,AB=5,求DC的长.
如图,已知AB与CD交于点E,AB与CD的夹角为45°,若∠B+∠C=225°,AC=3,DB=4,AB=5,求DC的长. 如图,在△ABC中,BC的垂直平分线DE将△ABC的面积分成1:3的两部分.请问E点是否为AB的中点?说明理由.
如图,在△ABC中,BC的垂直平分线DE将△ABC的面积分成1:3的两部分.请问E点是否为AB的中点?说明理由.