题目内容
在△ABC中，已知∠C＞∠B，求证：AB＞AC．
考点：三角形三边关系,等腰三角形的判定与性质
专题：证明题
分析：利用反证法来证明，分别证明AB=AC和AB＜AC，得出矛盾即可．
解答：证明：
假设AB＞AC不成立，则有AB≤AC，
（1）假设AB=AC则，∠C=∠B，与∠C＞∠B矛盾，AB=AC不成立；
（2）假设AC＞AB，
过A作AD=AB，D在AC线段内，
且∠ABD=∠ADB，
因为∠ADB=∠DBC+∠C，∠ABD+∠DBC=∠B，
则有∠B-∠C=2∠DBC＞0，
这是和∠C＞∠B矛盾的，AB＜AC不成立，
所以只能AB＞AC．
假设AB＞AC不成立，则有AB≤AC，
（1）假设AB=AC则，∠C=∠B，与∠C＞∠B矛盾，AB=AC不成立；
（2）假设AC＞AB，
过A作AD=AB，D在AC线段内，
且∠ABD=∠ADB，
因为∠ADB=∠DBC+∠C，∠ABD+∠DBC=∠B，
则有∠B-∠C=2∠DBC＞0，
这是和∠C＞∠B矛盾的，AB＜AC不成立，
所以只能AB＞AC．
点评：本题主要考查反证法，解题的关系是假设结论不成立，由结论的对立面找到矛盾．
练习册系列答案
相关题目
如图，在某山顶A处垂直于水平面有一高塔，塔高为（40
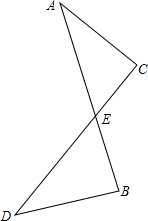如图，已知AB与CD交于点E，AB与CD的夹角为45°，若∠B+∠C=225°，AC=3，DB=4，AB=5，求DC的长．
如图，在△ABC中，BC的垂直平分线DE将△ABC的面积分成1：3的两部分．请问E点是否为AB的中点？说明理由．