题目内容
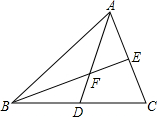 如图,△ABC中,AB=BC,AC=8,点F是△ABC的重心(即点F是△ABC的两条中线AD、BE的交点),BF=6,则DF=
如图,△ABC中,AB=BC,AC=8,点F是△ABC的重心(即点F是△ABC的两条中线AD、BE的交点),BF=6,则DF=考点:三角形的重心
专题:
分析:根据三角形的重心到顶点的距离等于到对边中点的距离的一半求出EF,再根据等腰三角形三线合一的性质求出AE,BE⊥AC,然后利用利用勾股定理列式求出AF,再次利用三角形的重心到顶点的距离等于到对边中点的距离的一半求解即可.
解答:解:∵点F是△ABC的重心,
∴EF=
BF=
×6=3,
∵AB=BC,BE是中线,
∴AE=
AC=
×8=4,BE⊥AC,
在Rt△AEF中,由勾股定理得,AF=
=
=5,
∴DF=
AF=
.
故答案为:
.
∴EF=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=BC,BE是中线,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△AEF中,由勾股定理得,AF=
| AE2+EF2 |
| 32+42 |
∴DF=
| 1 |
| 2 |
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
点评:本题考查了三角形的重心,等腰三角形三线合一的性质,勾股定理,熟记三角形的重心到顶点的距离等于到对边中点的距离的一半是解题的关键,此内容已经不作要求,此题可斟酌使用.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
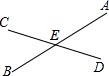 如图所示,直线AB、CD是两条交叉的公路,且交于点E,现在要建一个商店,要求它到两公路的距离相等且离点E300米处,则可供选择的地址有
如图所示,直线AB、CD是两条交叉的公路,且交于点E,现在要建一个商店,要求它到两公路的距离相等且离点E300米处,则可供选择的地址有
 校门口经常有人搞摸奖.在一只黑色的口袋里装有处颜色外都相同的50只小球,其中红球1只,黄球2只,绿球10只,其余为白球.搅拌均匀后,任意摸1个球.奖品的情况标注在球上.
校门口经常有人搞摸奖.在一只黑色的口袋里装有处颜色外都相同的50只小球,其中红球1只,黄球2只,绿球10只,其余为白球.搅拌均匀后,任意摸1个球.奖品的情况标注在球上.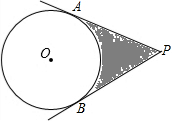 如图,已知PA、PB切⊙O于A、B两点,PO=4cm,∠APB=60°,求阴影部分的周长.
如图,已知PA、PB切⊙O于A、B两点,PO=4cm,∠APB=60°,求阴影部分的周长.