题目内容
计算
.
|
考点:解三元一次方程组
专题:计算题
分析:设方程组中第一个方程等于k,表示出x,y,z,代入第二个方程求出k的值,即可确定出方程组的解.
解答:解:设
=
=
=k,即x=2k,y=3k,z=4k,
代入2x+y-z=6中得:4k+3k-4k=6,
解得:k=2,
可得x=2k=4,y=3k=6,z=4k=8,
则方程组的解为
.
| x |
| 2 |
| y |
| 3 |
| z |
| 4 |
代入2x+y-z=6中得:4k+3k-4k=6,
解得:k=2,
可得x=2k=4,y=3k=6,z=4k=8,
则方程组的解为
|
点评:此题考查了解三元一次方程的组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
已知a∥b,b∥c,则直线a与c的关系是( )
| A、相交 | B、平行 |
| C、相交或平行 | D、垂直 |
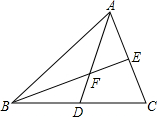 如图,△ABC中,AB=BC,AC=8,点F是△ABC的重心(即点F是△ABC的两条中线AD、BE的交点),BF=6,则DF=
如图,△ABC中,AB=BC,AC=8,点F是△ABC的重心(即点F是△ABC的两条中线AD、BE的交点),BF=6,则DF=