题目内容
10．
如图，网格纸上正方形小格的边长为1．图中线段AB和点P绕着同一个点做相同的旋转，分别得到线段A'B'和点P'，则点P'所在的单位正方形区域是（ ）| A． | 1区 | B． | 2区 | C． | 3区 | D． | 4区 |
分析 根据旋转的性质连接AA′、BB′，分别作AA′、BB′的中垂线，两直线的交点即为旋转中心，从而得出线段AB和点P是绕着同一个该点逆时针旋转90°，据此可得答案．
解答 解：如图，连接AA′、BB′，分别作AA′、BB′的中垂线，两直线的交点即为旋转中心，
由图可知，线段AB和点P绕着同一个该点逆时针旋转90°，
∴点P逆时针旋转90°后所得对应点P′落在4区，
故选：D．
点评 本题主要考查旋转，熟练掌握旋转的性质得出图形的旋转中心及旋转方向是解题的关键．
练习册系列答案
相关题目
20．
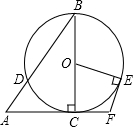如图，在Rt△ABC中，∠ACB=90°，∠A=56°．以BC为直径的⊙O交AB于点D．E是⊙O上一点，且$\widehat{C{E}}$=$\widehat{CD}$，连接OE．过点E作EF⊥OE，交AC的延长线于点F，则∠F的度数为（ ）
如图，在Rt△ABC中，∠ACB=90°，∠A=56°．以BC为直径的⊙O交AB于点D．E是⊙O上一点，且$\widehat{C{E}}$=$\widehat{CD}$，连接OE．过点E作EF⊥OE，交AC的延长线于点F，则∠F的度数为（ ）| A． | 92° | B． | 108° | C． | 112° | D． | 124° |
1．下列运算正确的是（ ）
| A． | a2•a3=a6 | B． | a8÷a2=a4 | C． | （a3）2=a5 | D． | （ab）2=a2b2 |
2016年11月1日，万众期待的歼20战机现身珠海航展，上午9时，某航空爱好者在地面C处测得点A处的歼20战机的仰角是30°，正以300米/秒的速度向正西方向航行，1分钟后到达点B处，此时航空爱好者测得其仰角为45°，如图所示，求歼20战机在珠海航展表演时的飞行高度．（精确到100米）参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73．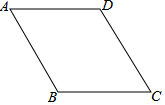
如图，在菱形ABCD中，∠ABC=120°，AB=10cm，点P是这个菱形内部或边上的一点．若以P，B，C为顶点的三角形是等腰三角形，则P，A（P，A两点不重合）两点间的最短距离为10$\sqrt{3}$-10cm．
2．-2的倒数是（ ）
| A． | 2 | B． | -2 | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
