题目内容
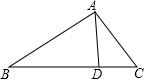 如图,点D是△ABC的边BC上一点,已知AC=3,CD=
如图,点D是△ABC的边BC上一点,已知AC=3,CD=| 2 |
考点:相似三角形的判定与性质
专题:
分析:首先证明△ACD∽△BCA,由相似三角形的性质:相似三角新的对应边的比相等即可求得BC的长,根据BD=BC-CD求解.
解答:解:∵∠DAC=∠B,∠C=∠C,
∴△ACD∽△BCA,
∴
=
,即
=
,
解得:BC=
,
则BD=BC-CD=
-
=
.
故答案是:
.
∴△ACD∽△BCA,
∴
| AC |
| BC |
| CD |
| AC |
| 3 |
| BC |
| ||
| 3 |
解得:BC=
9
| ||
| 2 |
则BD=BC-CD=
9
| ||
| 2 |
| 2 |
7
| ||
| 2 |
故答案是:
7
| ||
| 2 |
点评:本题考查了相似三角形的性质:相似三角新的对应边的比相等,证明△ACD∽△BCA是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
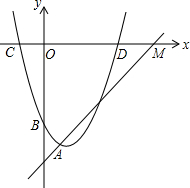 如图,抛物线y=x2-2x+c的顶点A在直线y=x-5上,直线与两坐标轴的交点分别为M和N,
如图,抛物线y=x2-2x+c的顶点A在直线y=x-5上,直线与两坐标轴的交点分别为M和N, 如图,AB是⊙O的直径,AB=10,圆心角∠AOC=60°,点D是
如图,AB是⊙O的直径,AB=10,圆心角∠AOC=60°,点D是
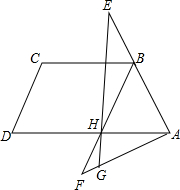 如图,等腰梯形ABCD中,AD∥BC,H是AD中点,AB=BC=CD=
如图,等腰梯形ABCD中,AD∥BC,H是AD中点,AB=BC=CD=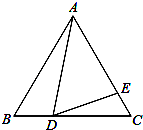 如图,在边长为9的等边△ABC中,BD=3,∠ADE=60°,求AE的长.
如图,在边长为9的等边△ABC中,BD=3,∠ADE=60°,求AE的长. 如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则△ACD的面积为
如图,四边形ABCD中,AC、BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,则△ACD的面积为 如图,已知AB=CD,AE=DF,CE=BF.
如图,已知AB=CD,AE=DF,CE=BF. 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动