题目内容
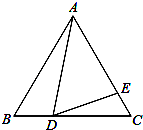 如图,在边长为9的等边△ABC中,BD=3,∠ADE=60°,求AE的长.
如图,在边长为9的等边△ABC中,BD=3,∠ADE=60°,求AE的长.考点:相似三角形的判定与性质,等边三角形的性质
专题:
分析:根据三角形的外角的性质证得∠DAB=∠EDC,则易证△ABD∽△DCE,根据相似三角形的性质,相似三角形的对应边的比相等即可求解.
解答:解:∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=BC,
∴CD=BC-BD=9-3=6,
∴∠BAD+∠ADB=120°,
∵∠ADE=60°,
∴∠ADB+∠EDC=120°,
∴∠DAB=∠EDC,
又∵∠B=∠C=60°,
∴△ABD∽△DCE,
则
=
,即
=
,
解得:CE=2,
故AE=AC-CE=9-2=7.
∴∠B=∠C=60°,AB=BC,
∴CD=BC-BD=9-3=6,
∴∠BAD+∠ADB=120°,
∵∠ADE=60°,
∴∠ADB+∠EDC=120°,
∴∠DAB=∠EDC,
又∵∠B=∠C=60°,
∴△ABD∽△DCE,
则
| AB |
| BD |
| DC |
| CE |
| 9 |
| 3 |
| 6 |
| CE |
解得:CE=2,
故AE=AC-CE=9-2=7.
点评:本题考查了相似三角形的判定与性质,正确利用三角形的外角的性质,证明∠DAB=∠EDC是关键.

练习册系列答案
相关题目
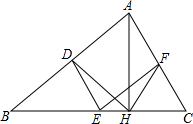 如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.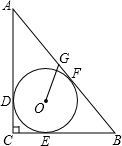 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,⊙O为△ABC内切圆,与三边分别相切于D、E、F.
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,⊙O为△ABC内切圆,与三边分别相切于D、E、F.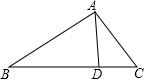 如图,点D是△ABC的边BC上一点,已知AC=3,CD=
如图,点D是△ABC的边BC上一点,已知AC=3,CD=
 如图,AD是△ABC的角平分线,过点D分别作AC和AB的平行线,交AB于点E,交AC于点F.求证:四边形AEDF是菱形.
如图,AD是△ABC的角平分线,过点D分别作AC和AB的平行线,交AB于点E,交AC于点F.求证:四边形AEDF是菱形.