题目内容
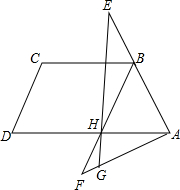 如图,等腰梯形ABCD中,AD∥BC,H是AD中点,AB=BC=CD=
如图,等腰梯形ABCD中,AD∥BC,H是AD中点,AB=BC=CD=| 1 |
| 2 |
考点:相似三角形的判定与性质,全等三角形的判定与性质,等腰梯形的性质
专题:证明题
分析:首先证明四边形CBHD是平行四边形,则可以证得△ABH是等边三角形,然后证明△EBH≌△FHA,从而证明∠EGA=∠EAH,则△EAH∽△EGA,根据相似三角形的对应边的比相等证得.
解答:证明:∵AB=BC=CD=
AD,HD=HA,
∴BC∥DH,BC=DH,
∴四边形CBHD是平行四边形,
∴BH=DC=AB=AH,
∴△ABH是等边三角形,
∴∠ABH=∠AHB=∠BHA=60°,
∴∠EBH=∠FHA.
则在△EBH和△FHA中,
,
∴△EBH≌△FHA(SAS),
∴∠FAH=∠EHB,
∵∠EHA=∠HGA+∠HAF,
∴∠EGA=60°=∠EAH,∠E=∠E,
∴△EAH∽△EGA,
∴
=
,
∴AE2=EH•EG.
| 1 |
| 2 |

∴BC∥DH,BC=DH,
∴四边形CBHD是平行四边形,
∴BH=DC=AB=AH,
∴△ABH是等边三角形,
∴∠ABH=∠AHB=∠BHA=60°,
∴∠EBH=∠FHA.
则在△EBH和△FHA中,
|
∴△EBH≌△FHA(SAS),
∴∠FAH=∠EHB,
∵∠EHA=∠HGA+∠HAF,
∴∠EGA=60°=∠EAH,∠E=∠E,
∴△EAH∽△EGA,
∴
| EA |
| EG |
| EH |
| EA |
∴AE2=EH•EG.
点评:本题考查了全等三角形的判定与性质以及相似三角形的判定与性质,证明等积式的问题,常用的方法是证明三角形相似.

练习册系列答案
相关题目
 已知:如图,抛物线y=ax2+bx+c经过A(1,0),B(5,0),C(0,5)三点.
已知:如图,抛物线y=ax2+bx+c经过A(1,0),B(5,0),C(0,5)三点.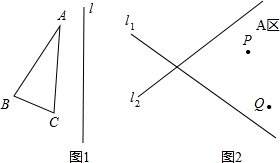 (1)画出图1中△ABC关于直线L的对称图形△A′B′C′.
(1)画出图1中△ABC关于直线L的对称图形△A′B′C′.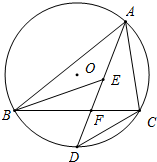 如图,已知△ABC内接于⊙O,AD平分∠BAC交BC于点F,交⊙O于点D,E是△ABC内心,连BE.
如图,已知△ABC内接于⊙O,AD平分∠BAC交BC于点F,交⊙O于点D,E是△ABC内心,连BE.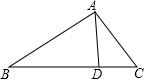 如图,点D是△ABC的边BC上一点,已知AC=3,CD=
如图,点D是△ABC的边BC上一点,已知AC=3,CD=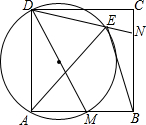 如图,在正方形ABCD中,M、N分别是AB、BC边上的两个动点,且∠MDN=45°,以DM为直径的圆交DN于点E,连结BE、AE.
如图,在正方形ABCD中,M、N分别是AB、BC边上的两个动点,且∠MDN=45°,以DM为直径的圆交DN于点E,连结BE、AE.