题目内容
 如图,AB是⊙O的直径,AB=10,圆心角∠AOC=60°,点D是
如图,AB是⊙O的直径,AB=10,圆心角∠AOC=60°,点D是 |
| AC |
考点:轴对称-最短路线问题,勾股定理,垂径定理
专题:
分析:作点C关于AB的对称点C′,根据轴对称确定最短路线问题,连接C′D,C′D与AB的交点即为使PC+PD的值最小的点,此时PC+PD=C′D,连接OC′、OD,求出∠C′OD=90°,再根据等腰直角三角形的斜边等于直角边的
倍解答.
| 2 |
解答: 解:如图,作点C关于AB的对称点C′,连接C′D,
解:如图,作点C关于AB的对称点C′,连接C′D,
则C′D与AB的交点即为使PC+PD的值最小的点,此时PC+PD=C′D,
连接OC′、OD,
∵∠AOC=60°,
∴∠AOC′=60°,
∵点D是
的中点,
∴∠AOD=
∠AOC=
×60°=30°,
∴∠C′OD=30°+60°=90°,
∴△C′OD是等腰直角三角形,
∵直径AB=10,
∴半径OD=
×10=5,
∴C′D=
OD=5
,
即PC+PD的最小值是5
.
故答案为:5
.
 解:如图,作点C关于AB的对称点C′,连接C′D,
解:如图,作点C关于AB的对称点C′,连接C′D,则C′D与AB的交点即为使PC+PD的值最小的点,此时PC+PD=C′D,
连接OC′、OD,
∵∠AOC=60°,
∴∠AOC′=60°,
∵点D是
 |
| AC |
∴∠AOD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠C′OD=30°+60°=90°,
∴△C′OD是等腰直角三角形,
∵直径AB=10,
∴半径OD=
| 1 |
| 2 |
∴C′D=
| 2 |
| 2 |
即PC+PD的最小值是5
| 2 |
故答案为:5
| 2 |
点评:本题考查了轴对称确定最短路线问题,垂径定理,等腰直角三角形的判定与性质,熟练掌握各性质并确定出点P的位置是解题的关键,难点在于作辅助线构造出等腰直角三角形.

练习册系列答案
相关题目
在下列四组数中,不是勾股数的一组数是( )
| A、a=15,b=8,c=17 |
| B、a=9,b=12,c=15 |
| C、a=0.3,b=0.5,c=0.4 |
| D、a=7,b=24,c=25 |
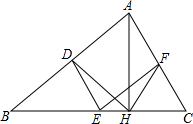 如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.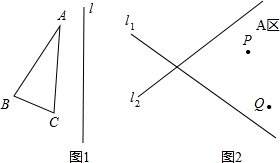 (1)画出图1中△ABC关于直线L的对称图形△A′B′C′.
(1)画出图1中△ABC关于直线L的对称图形△A′B′C′.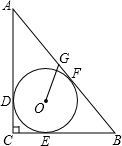 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,⊙O为△ABC内切圆,与三边分别相切于D、E、F.
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,⊙O为△ABC内切圆,与三边分别相切于D、E、F.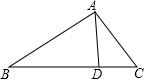 如图,点D是△ABC的边BC上一点,已知AC=3,CD=
如图,点D是△ABC的边BC上一点,已知AC=3,CD=