题目内容
10.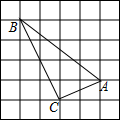 如图,每个小正方形的边长都为1.
如图,每个小正方形的边长都为1.(1)求△ABC的面积与周长;
(2)∠ACB是直角吗?
分析 (1)根据图形,△ABC的面积等于矩形的面积减去3个直角三角形的面积,根据勾股定理得到△ABC的三边长,再根据三角形周长的定义求出△ABC的周长.
(2)根据勾股定理的逆定理可判断△ABC的形状.
解答 解:(1)△ABC的面积=4×4-$\frac{1}{2}$×(2×1+2×4+4×3)=5;
由勾股定理可得:AC=$\sqrt{5}$,BC=2$\sqrt{5}$,AB=5,
则△ABC的周长是$\sqrt{5}$+2$\sqrt{5}$+5=3$\sqrt{5}$+5;
(2)∵AC2+BC2=5+20=25,AB2=25,
∴AC2+BC2=AB2,
∴△ABC的形状是直角三角形,∠ACB是直角.
点评 本题考查了勾股定理以及其逆定理的运用,解题的关键是善于把不规则图形的面积转化为规则图形的面积.

练习册系列答案
相关题目
19. 如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )
如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )
 如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )
如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )| A. | 1.5 | B. | 2.5 | C. | 2.25 | D. | 3 |
19.已知点A、B的坐标分别为(1,0)、(2,0).若顶点在x轴下方的二次函数y=x2+(a-3)x+3的图象与线段AB恰好只有一个交点,则a的取值范围( )
| A. | $-1≤a<-\frac{1}{2}$ | B. | $-1≤a≤\frac{1}{2}$ | C. | $\frac{1}{2}<a<2$ | D. | -1<a≤1 |
20.下列说法中错误的是( )
| A. | 不等式x+1≤4的整数解有无数个 | B. | 不等式x+4<5的解集是x<1 | ||
| C. | 不等式x<4的正整数解为有限个 | D. | 0是不等式3x<-1的解 |
 如图正方形网格中,小正方形的边长为1,△ABC的顶点在格点上,判断△ABC是否是直角三角形?并说明理由.
如图正方形网格中,小正方形的边长为1,△ABC的顶点在格点上,判断△ABC是否是直角三角形?并说明理由.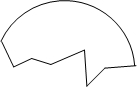 一个破圆轮残片如图所示,现要修复该圆轮,怎样确定这个圆轮残片的圆心和半径?(写出找圆心和半径的步骤)
一个破圆轮残片如图所示,现要修复该圆轮,怎样确定这个圆轮残片的圆心和半径?(写出找圆心和半径的步骤)