Question

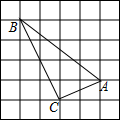
5．如图正方形网格中，小正方形的边长为1，△ABC的顶点在格点上，判断△ABC是否是直角三角形？并说明理由．

Answer 1

分析 根据勾股定理求得△ABC各边的长，再利用勾股定理的逆定理进行判定，从而得到其形状．

解答 解：∵小正方形的边长为1，
∴AC²=2²+3²=13，AB²=4²+6²=52，BC²=1²+8²=65，
∵在△ABC中，AC²+AB²=13+52=65，BC²=65，
∴AB²+BC²=AC²，
∴△ABC是直角三角形．

点评 本题主要考查勾股定理和勾股定理的逆定理的应用，要判断一个角是不是直角，先要构造出三角形，然后知道三条边的大小，用较小的两条边的平方和与最大的边的平方比较，如果相等，则三角形为直角三角形．