题目内容
19.已知点A、B的坐标分别为(1,0)、(2,0).若顶点在x轴下方的二次函数y=x2+(a-3)x+3的图象与线段AB恰好只有一个交点,则a的取值范围( )| A. | $-1≤a<-\frac{1}{2}$ | B. | $-1≤a≤\frac{1}{2}$ | C. | $\frac{1}{2}<a<2$ | D. | -1<a≤1 |
分析 由顶点在x轴下方的二次函数以及图象与线段AB恰好只有一个交点可得到关于a的不等式组,解不等式组即可得到a的取值范围.
解答 解:由题意可得:
若yx=1<0且yx=2≥0,即
$\left\{\begin{array}{l}{1+(a-3)+3<0}\\{4+2(a-3)+3≥0}\end{array}\right.$,解得此不等式组无解;
若yx=2<0且yx=1≥0,即
$\left\{\begin{array}{l}{1+(a-3)+3≥0}\\{4+2(a-3)+3<0}\end{array}\right.$,解得-1≤a<-$\frac{1}{2}$,
故选B.
点评 本题考查了抛物线与x轴交点的问题,涉及二次函数的综合性质,关键是当二次函数顶点在x轴下方或当二次函数的顶点在x轴上时分析结果不一样.

练习册系列答案
相关题目
8.估计$\sqrt{14}$的值在哪两个数之间( )
| A. | 1与2 | B. | 2 与3 | C. | 3与4 | D. | 4与5 |
14.已知ax2+2x+14=2x2-2x+3a是关于x的一元一次方程,则其解是( )
| A. | x=-2 | B. | x=$\frac{1}{2}$ | C. | x=-$\frac{1}{2}$ | D. | x=2 |
4.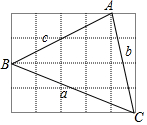 如图所示,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC(△ABC的各项点均在格点上)的三边a、b、c之间的大小关系是( )
如图所示,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC(△ABC的各项点均在格点上)的三边a、b、c之间的大小关系是( )
 如图所示,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC(△ABC的各项点均在格点上)的三边a、b、c之间的大小关系是( )
如图所示,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC(△ABC的各项点均在格点上)的三边a、b、c之间的大小关系是( )| A. | c<a<b | B. | b<c<a | C. | c<b<a | D. | a<c<b |
8. 如图,下列条件中,能判断AB∥CD的是( )
如图,下列条件中,能判断AB∥CD的是( )
 如图,下列条件中,能判断AB∥CD的是( )
如图,下列条件中,能判断AB∥CD的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠BAC=∠BCD | D. | ∠ABC+∠BAD=180° |
9.如果a=(-2009)0,b=(-0.1)-1,c=(-$\frac{5}{3}$)-2,那么a、b、c的大小关系为( )
| A. | a>b>c | B. | c>a>b | C. | c>b>a | D. | a>c>b |
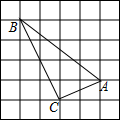 如图,每个小正方形的边长都为1.
如图,每个小正方形的边长都为1.