题目内容
13.某校九年级共有四个班,各班人数比例如图1所示.在一次数学考试中,四个班的平均成绩如图2所示.
(1)四个班平均成绩的中位数是69;
(2)下列说法:①3班85分以上人数最少;②1,3两班的平均分差距最小;③本次考试年段成绩最高的学生在4班.其中正确的是②(填序号);
(3)若用公式$\overline x=\frac{m+n}{2}$(m,n分别表示各班平均成绩)分别计算1,2两班和3,4两班的平均成绩,哪两班的计算结果会与实际平均成绩相同,请说明理由.
分析 (1)根据图2中数据结合中位数定义求解可得;
(2)由图2中数据可知;
(3)分别根据题意计算方法和加权平均数的计算方法计算后比较可得.
解答 解:(1)四个班平均成绩的中位数是$\frac{67+71}{2}$=69,
故答案为:69;
(2)根据四个班的平均成绩无法判断85分以上人数、年级成绩最高的学生,故①③错误,1,3两班的平均分差距最小,为2分,故②正确,
故答案为:②;
(3)1、2两班平均成绩为$\frac{67+71}{2}$=69,
设总人数为n,则1、2两班实际平均成绩为$\frac{n•a%•67+n•b%•71}{n•a%+n•b%}$,
∴1、2两班的计算结果与实际平均成绩不相同;
3、4两班的平均成绩为$\frac{65+74}{2}$=69.5,
3、4两班实际平均成绩$\frac{n•c%•65+n•c%•74}{n•c%+n•c%}$=69.5,
∴3、4两班的计算结果与实际平均成绩相同.
点评 本题主要考查条形统计图和中位数、平均数的计算,熟练掌握加权平均数的计算方法是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
17. 如图所示,在△ABC中,D是BC的中点,DE⊥BC交AC于点E,已知AD=AB,连接BE交AD于点F,下列结论:①BE=CE;②∠CAD=∠ABE;③S△ABF=3S△DEF;④△DEF∽△DAE,其中正确的有( )
如图所示,在△ABC中,D是BC的中点,DE⊥BC交AC于点E,已知AD=AB,连接BE交AD于点F,下列结论:①BE=CE;②∠CAD=∠ABE;③S△ABF=3S△DEF;④△DEF∽△DAE,其中正确的有( )
 如图所示,在△ABC中,D是BC的中点,DE⊥BC交AC于点E,已知AD=AB,连接BE交AD于点F,下列结论:①BE=CE;②∠CAD=∠ABE;③S△ABF=3S△DEF;④△DEF∽△DAE,其中正确的有( )
如图所示,在△ABC中,D是BC的中点,DE⊥BC交AC于点E,已知AD=AB,连接BE交AD于点F,下列结论:①BE=CE;②∠CAD=∠ABE;③S△ABF=3S△DEF;④△DEF∽△DAE,其中正确的有( )| A. | 1个 | B. | 4个 | C. | 3个 | D. | 2个 |
2. 如图,在一块宽为20m,长为32m的矩形空地上,修筑宽相等的两条小路,两条路分别与矩形的边平行,如图,若使剩余(阴影)部分的面积为560m2,问小路的宽应是多少?设小路的宽为xcm,根据题意得( )
如图,在一块宽为20m,长为32m的矩形空地上,修筑宽相等的两条小路,两条路分别与矩形的边平行,如图,若使剩余(阴影)部分的面积为560m2,问小路的宽应是多少?设小路的宽为xcm,根据题意得( )
 如图,在一块宽为20m,长为32m的矩形空地上,修筑宽相等的两条小路,两条路分别与矩形的边平行,如图,若使剩余(阴影)部分的面积为560m2,问小路的宽应是多少?设小路的宽为xcm,根据题意得( )
如图,在一块宽为20m,长为32m的矩形空地上,修筑宽相等的两条小路,两条路分别与矩形的边平行,如图,若使剩余(阴影)部分的面积为560m2,问小路的宽应是多少?设小路的宽为xcm,根据题意得( )| A. | 32x+20x=20×32-560 | B. | 32×20-20x×32x=560 | ||
| C. | (32-x)(20-x)=560 | D. | 以上都不正确 |
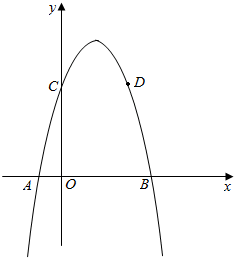 已知:抛物线y=-x2+bx+c的图象交y轴于C,交x轴交于A、B两点,抛物线经过点D(4,5),C、D两点关于抛物线的对称轴对称.
已知:抛物线y=-x2+bx+c的图象交y轴于C,交x轴交于A、B两点,抛物线经过点D(4,5),C、D两点关于抛物线的对称轴对称.
 菱形ABCD中,∠B=60°,延长BC至E,使得CE=BC,点F在DE上,DF=6,AG平分∠BAF,与线段BC相交于点G,若CG=2,则线段AB的长度为10.
菱形ABCD中,∠B=60°,延长BC至E,使得CE=BC,点F在DE上,DF=6,AG平分∠BAF,与线段BC相交于点G,若CG=2,则线段AB的长度为10. 在如图的正方形网格中,有一个格点三角形ABC(即三角形的顶点都在格点上).
在如图的正方形网格中,有一个格点三角形ABC(即三角形的顶点都在格点上).