题目内容
2．
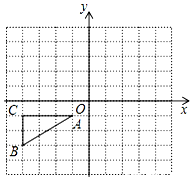如图，已知△ABC的顶点A，B，C的坐标分别是A（-1，-1），B（-4，-3），C（-4，-1）（1）作出△ABC关于原点O中心对称的图形△A1B1C1，画出△A1B1C1；
（2）将△ABC绕原点O按顺时针方向旋转90°后得到△A2B2C2，画出△A2B2C2．
分析 （1）分别作出各点关于原点的对称点，再顺次连接即可；
（2）根据图形旋转的性质画出△A2B2C2即可．
解答 
解：（1）如图，△A1B1C1即为所求；
（2）如图，△A2B2C2即为所求．
点评 本题考查的是作图-旋转变换，熟知图形旋转不变性的性质是解答此题的关键．
练习册系列答案
相关题目
13．一个正三角形的边长为2，它的高是（ ）
| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{4}$ |
10．下列等式中，成立的是（ ）
| A． | （a+b）2=a2+b2 | B． | （a-b）2=a2-b2 | C． | （-a-b）2=a2-2ab+b2 | D． | （-a-b）（a-b）=b2-a2 |
12．∑表示数学中的求和符号，主要用于求多个数的和，∑下面的小字，i=1表示从1开始求和；上面的小字，如n表示求和到n为止．即$\sum_{i=1}^{n}$xi=x1+x2+x3+…+xn．则$\sum_{i=1}^{n}$（i2-i）表示（ ）
| A． | n2-1 | B． | 12+22+32+…+i2-i | ||
| C． | 12+22+32+…+n2-1 | D． | 12+22+32+…+n2-（1+2+3+…+n ） |