题目内容
14.计算或化简:(1)($\frac{2}{3}$)-1+(π-3)0-(-2)-2
(2)(-2a)3+(a4)2÷(-a)5
(3)(p-q)4÷(q-p)3•(p-q)5
(4)(2a+b)(2b-a)
分析 (1)首先计算乘方,然后从左向右依次计算即可.
(2)首先计算乘方,然后计算除法和加法即可.
(3)首先计算除法,然后计算乘法即可.
(4)根据多项式乘多项式的运算方法计算即可.
解答 解:(1)($\frac{2}{3}$)-1+(π-3)0-(-2)-2
=1.5+1-0.25
=2.25
(2)(-2a)3+(a4)2÷(-a)5
=-8a3+a8÷(-a5)
=-8a3-a3
=-9a3
(3)(p-q)4÷(q-p)3•(p-q)5
=-(p-q)•(p-q)5
=-(p-q)6
(4)(2a+b)(2b-a)
=4ab-2a2+2b2-ab
=3ab-2a2+2b2
点评 此题主要考查了整式的混合运算,实数的运算方法,以及零指数幂、负整数指数幂的运算方法,要熟练掌握,解答此题的关键是要明确:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.

练习册系列答案
相关题目
4.我市努力打造“美丽南宁•生态南宁”建设,环境建设取得更大发展,近七天的空气质量指数为优等级,分别是:28,45,28,45,28,30,53,这组数据的众数是( )
| A. | 28 | B. | 30 | C. | 45 | D. | 53 |
6.如图,它们是按一定规律排列的,依照此规律,第20个图形共有★的数量为( )

| A. | 63 | B. | 57 | C. | 68 | D. | 60 |
3.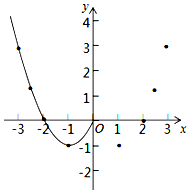 某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下.
某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下.
(1)自变量x的取值范围是全体实数,x与y的几组对应值如下:
其中,m=0.
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请你画出该函数图象的另一部分.
(3)观察函数图象,写出一条性质.函数y=x2-2|x|的图象关于y轴对称
(4)进一步探究函数图象发现:
①方程x2-2|x|=0有3个实数根;
②关于x的方程x2-2|x|=a有4个实数根时,a的取值范围是-1<a<0.
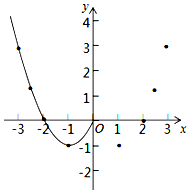 某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下.
某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下.(1)自变量x的取值范围是全体实数,x与y的几组对应值如下:
| x | … | -3 | -$\frac{5}{2}$ | -2 | -1 | 0 | 1 | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | 3 | $\frac{5}{4}$ | m | -1 | 0 | -1 | 0 | $\frac{5}{4}$ | 3 | … |
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请你画出该函数图象的另一部分.
(3)观察函数图象,写出一条性质.函数y=x2-2|x|的图象关于y轴对称
(4)进一步探究函数图象发现:
①方程x2-2|x|=0有3个实数根;
②关于x的方程x2-2|x|=a有4个实数根时,a的取值范围是-1<a<0.
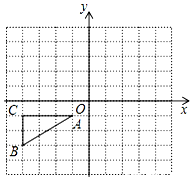 如图,已知△ABC的顶点A,B,C的坐标分别是A(-1,-1),B(-4,-3),C(-4,-1)
如图,已知△ABC的顶点A,B,C的坐标分别是A(-1,-1),B(-4,-3),C(-4,-1)