题目内容
13.一个正三角形的边长为2,它的高是( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
分析 根据等边三角形三线合一的性质,即可得∴∠BAD=$\frac{1}{2}$∠BAC=30°,解直角三角形即可求AD的值.
解答 解:∵△ABC是等边三角形,AD⊥BC,
∴AD是∠BAC的平分线,
∴∠BAD=$\frac{1}{2}$∠BAC=30°,
∴,AD=sin30°•BC=$\frac{\sqrt{3}}{2}$×2=$\sqrt{3}$,
故选A.
点评 本题考查了等边三角形三线合一的性质,本题中解直角三角形求AD的值是解题的关键.

练习册系列答案
相关题目
4.我市努力打造“美丽南宁•生态南宁”建设,环境建设取得更大发展,近七天的空气质量指数为优等级,分别是:28,45,28,45,28,30,53,这组数据的众数是( )
| A. | 28 | B. | 30 | C. | 45 | D. | 53 |
1.下列计算错误的有( )
(1)(2x+y)2=4x2+y2
(2)(-x-y)2=x2-2xy+y2
(3)(x-$\frac{1}{2}$)2=x2-2x+$\frac{1}{4}$
(4)(3b-a)(-3b-a)=a2-9b2.
(1)(2x+y)2=4x2+y2
(2)(-x-y)2=x2-2xy+y2
(3)(x-$\frac{1}{2}$)2=x2-2x+$\frac{1}{4}$
(4)(3b-a)(-3b-a)=a2-9b2.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.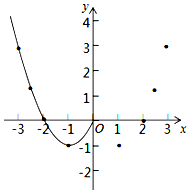 某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下.
某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下.
(1)自变量x的取值范围是全体实数,x与y的几组对应值如下:
其中,m=0.
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请你画出该函数图象的另一部分.
(3)观察函数图象,写出一条性质.函数y=x2-2|x|的图象关于y轴对称
(4)进一步探究函数图象发现:
①方程x2-2|x|=0有3个实数根;
②关于x的方程x2-2|x|=a有4个实数根时,a的取值范围是-1<a<0.
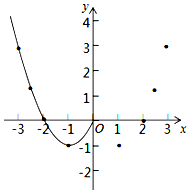 某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下.
某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下.(1)自变量x的取值范围是全体实数,x与y的几组对应值如下:
| x | … | -3 | -$\frac{5}{2}$ | -2 | -1 | 0 | 1 | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | 3 | $\frac{5}{4}$ | m | -1 | 0 | -1 | 0 | $\frac{5}{4}$ | 3 | … |
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请你画出该函数图象的另一部分.
(3)观察函数图象,写出一条性质.函数y=x2-2|x|的图象关于y轴对称
(4)进一步探究函数图象发现:
①方程x2-2|x|=0有3个实数根;
②关于x的方程x2-2|x|=a有4个实数根时,a的取值范围是-1<a<0.
 △ABC中,∠A=62°,O是边AB和边BC的垂直平分线的交点,那么∠BCO=28°.
△ABC中,∠A=62°,O是边AB和边BC的垂直平分线的交点,那么∠BCO=28°.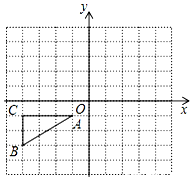 如图,已知△ABC的顶点A,B,C的坐标分别是A(-1,-1),B(-4,-3),C(-4,-1)
如图,已知△ABC的顶点A,B,C的坐标分别是A(-1,-1),B(-4,-3),C(-4,-1)