题目内容
7.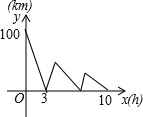 甲、乙两车分别从A、B两地同时出发,相向而行,甲车从A地行驶到B地后,立即按原速度返回A地,乙车从B地行驶到A地,两车到达A地均停止运动.两车之间的距离y(单位:千米)与乙车行驶时间x(单位:小时)之间的函数关系如图所示,问两车第二次相遇时乙车行驶的时间为$\frac{15}{2}$小时.
甲、乙两车分别从A、B两地同时出发,相向而行,甲车从A地行驶到B地后,立即按原速度返回A地,乙车从B地行驶到A地,两车到达A地均停止运动.两车之间的距离y(单位:千米)与乙车行驶时间x(单位:小时)之间的函数关系如图所示,问两车第二次相遇时乙车行驶的时间为$\frac{15}{2}$小时.
分析 先根据函数图象提供的信息,求得乙车的速度和甲车的速度,再根据甲车到达B地需要的时间,求得乙车行驶的距离,最后根据甲车返回后与乙车第二次相遇,求得所需的时间即可.
解答  解:根据函数图象可得,A、B两地相距100km,乙车从B地行驶到A地用10h,
解:根据函数图象可得,A、B两地相距100km,乙车从B地行驶到A地用10h,
∴乙车的速度v乙=100÷10=10(km/h),
根据两车第一次相遇用3h可得,甲车的速度v甲=$\frac{100}{3}$-10=$\frac{70}{3}$(km/h),
∴甲车到达B地需要:100÷$\frac{70}{3}$=$\frac{30}{7}$(h),
此时,乙车行驶的距离为:10×$\frac{30}{7}$=$\frac{300}{7}$(km),
设甲车从B地返回与乙车再次相遇需要t小时,
依题意得$\frac{70}{3}$t=10t+$\frac{300}{7}$,
解得t=$\frac{45}{14}$,
∴两车第二次相遇时乙车行驶的时间为:$\frac{45}{14}$+$\frac{30}{7}$=$\frac{15}{2}$.
故答案为:$\frac{15}{2}$
点评 本题以行程问题为背景,主要考查了一次函数的应用,解决问题的关键是根据函数图象获得关键的信息进行计算求解.在相遇问题中,要注意区分相向而行和同向而行不同的计算方式.

练习册系列答案
相关题目
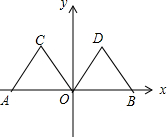 如图,在平面直角坐标系中,点A的坐标为(-2,0),等边△AOC经过平移或轴对称或旋转都可以得到△OBD.
如图,在平面直角坐标系中,点A的坐标为(-2,0),等边△AOC经过平移或轴对称或旋转都可以得到△OBD. 如图,在?ABCD中,AE﹕EB=1﹕2,
如图,在?ABCD中,AE﹕EB=1﹕2,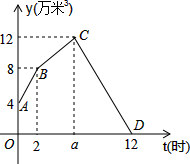 某水电站兴建了一个最大蓄水容量为12万米3的蓄水池,并配有2个流量相同的进水口和1个出水口.某天从0时至12时,进行机组试运行.其中,0时至2时打开2个进水口进水;2时,关闭1个进水口减缓进水速度,至蓄水池中水量达到最大蓄水容量后,随即关闭另一个进水口,并打开出水口,直至12时蓄水池中的水放完为止.若这3个水口的水流都是匀速的,水池中的蓄水量y(万米3)与时间t(时)之间的关系如图所示,请根据图象解决下列问题:
某水电站兴建了一个最大蓄水容量为12万米3的蓄水池,并配有2个流量相同的进水口和1个出水口.某天从0时至12时,进行机组试运行.其中,0时至2时打开2个进水口进水;2时,关闭1个进水口减缓进水速度,至蓄水池中水量达到最大蓄水容量后,随即关闭另一个进水口,并打开出水口,直至12时蓄水池中的水放完为止.若这3个水口的水流都是匀速的,水池中的蓄水量y(万米3)与时间t(时)之间的关系如图所示,请根据图象解决下列问题: 如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.
如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.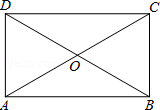 如图,在?ABCD中,对角线AC,BD相交于点O,且OA=OB.
如图,在?ABCD中,对角线AC,BD相交于点O,且OA=OB.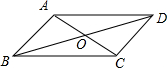 已知?ABCD,边AB=4,AD=8;对角线AC=6,BD=10,则OA=3,BD=5,周长=24.
已知?ABCD,边AB=4,AD=8;对角线AC=6,BD=10,则OA=3,BD=5,周长=24.