题目内容
17.某房地产开发公司计划建甲、乙两种户型的住房共80套,该公司所用建房资金不少于2850万元,甲种户型每套成本和售价分别为45万元和51万元,乙种户型每套成本和售价分别为30万元和35万元.设计划建甲种户型x套.(1)该公司最少建甲种户型多少套?
(2)若甲种户型不超过32套,选择哪种建房方案,该公司获利最大?最大利润是多少?
(3)在(2)的条件下,根据国家房地产政策,公司计划每套甲种户型住房的售价降低a万元(0<a≤1.5),乙种户型住房的售价不变,且预计所建的两种住房能全部售出,直接写出该公司获得最大利润的方案.
分析 (1)设公司建甲种户型x套,则B种户型(80-x)套,根据该公司所用建房资金不少于2850万元,列出不等式,进行求解即可;
(2)设所获得利润为W万元,根据一套的利润×总的套数=总利润,列出一次函数,再根据函数的增减性即可得出答案;
(3)分两种情况讨论:当0<a<1和1<a<1.5时,分别得出甲住房和乙住房各多少套时,该公司才能获得最大利润.
解答 解:(1)设公司建甲种户型x套,则B种户型(80-x)套,
45x+30(80-x)≥2850
解得:x≥30,
答:公司最少建甲种户型30套;
(2)设所获得利润为W万元,根据题意得:
W=(51-45)x+(35-30)(80-x)
=x+400,
∵k=1>0,
∴W随x的增大而增大,
∴当x取最大值32时,W有最大值432万元;
(3)当0<a<1时,甲住房有32套,乙住房有48套,该公司才能获得最大利润;
当1<a<1.5时,甲住房有30套,乙住房有50套,该公司才能获得最大利润;
点评 此题考查了一元一次不等式的应用和一次函数的应用,读懂题意,找出它们之间的数量关系,列出不等式或一次函数,掌握函数的增减性是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
12.利用加减消元法解方程组$\left\{\begin{array}{l}{2x+5y=3①}\\{5x-3y=6②}\end{array}\right.$,下列做法正确的是( )
| A. | 要消去y,可以将①×5+②×2 | B. | 要消去x,可以将①×3+②×(-5) | ||
| C. | 要消去y,可以将①×5+②×3 | D. | 要消去x,可以将①×(-5)+②×2 |
6.大家知道:“距离地面越远,温度越低”.小明查阅资料得到下面表格中的对应数据:
根据表中,请你帮助小明解决下列问题:
(1)根据表格中的数据发现:距离地面高度每升高1km,温度就降低6℃,进而猜想:温度T与距离地面高度h之间的函数关系式为T=20-6h.
(2)当h=10km时,高空的温度T是多少?
(3)当T=-28℃时,距离地面的高度h是多少?
| 距离地面高度h/km | 0 | 1 | 2 | 3 | 4 | 5 | … |
| 温度T/℃ | 20 | 14 | 8 | 2 | -4 | -10 | … |
(1)根据表格中的数据发现:距离地面高度每升高1km,温度就降低6℃,进而猜想:温度T与距离地面高度h之间的函数关系式为T=20-6h.
(2)当h=10km时,高空的温度T是多少?
(3)当T=-28℃时,距离地面的高度h是多少?
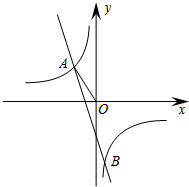 已知反比例函数y=$\frac{k_1}{3x}$的图象与一次函数y=k2x+m的图象交于A(a,1)、B($\frac{1}{3}$,-3)两点,连结AO.
已知反比例函数y=$\frac{k_1}{3x}$的图象与一次函数y=k2x+m的图象交于A(a,1)、B($\frac{1}{3}$,-3)两点,连结AO.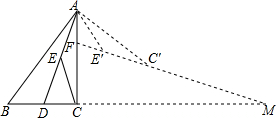 在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AD平分∠CAB交BC于点D,E为AD的中点,连接CE,将△ACE绕点A逆时针旋转至△AE′C′,直线E′C′交AC于点F,交BC的延长线于点M,若AF=E′F,则CM=$\frac{96-10\sqrt{10}}{7}$.
在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AD平分∠CAB交BC于点D,E为AD的中点,连接CE,将△ACE绕点A逆时针旋转至△AE′C′,直线E′C′交AC于点F,交BC的延长线于点M,若AF=E′F,则CM=$\frac{96-10\sqrt{10}}{7}$.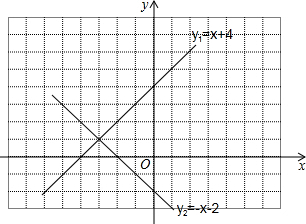 在同一平面直角坐标系内画直线y1=x+4和y2=-x-2图象,根据图象回答:
在同一平面直角坐标系内画直线y1=x+4和y2=-x-2图象,根据图象回答: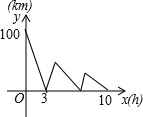 甲、乙两车分别从A、B两地同时出发,相向而行,甲车从A地行驶到B地后,立即按原速度返回A地,乙车从B地行驶到A地,两车到达A地均停止运动.两车之间的距离y(单位:千米)与乙车行驶时间x(单位:小时)之间的函数关系如图所示,问两车第二次相遇时乙车行驶的时间为$\frac{15}{2}$小时.
甲、乙两车分别从A、B两地同时出发,相向而行,甲车从A地行驶到B地后,立即按原速度返回A地,乙车从B地行驶到A地,两车到达A地均停止运动.两车之间的距离y(单位:千米)与乙车行驶时间x(单位:小时)之间的函数关系如图所示,问两车第二次相遇时乙车行驶的时间为$\frac{15}{2}$小时.