题目内容
15. 如图,在?ABCD中,AE﹕EB=1﹕2,
如图,在?ABCD中,AE﹕EB=1﹕2,(1)求△AEF与△CDF的周长的比;
(2)如果S△AEF=5cm2,求S△CDF.
分析 (1)易证△AEF∽△CDF,由相似三角形的性质:周长之比等于相似比即可求出△AEF与△CDF的周长的比;
(2)由(1)可知△AEF∽△CDF,由相似三角形的性质:面积之比等于相似比的平方即可求出问题答案.
解答 解:(1)∵AE﹕EB=1﹕2,
∴AE﹕AB=1﹕3,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△AEF∽△CDF
∴C△AEF﹕C△CDF=AE﹕CD=AE﹕AB=1﹕3,
(2)由(1)△AEF∽△CDF
∴S△AEF﹕S△CDF=(AE﹕CD)2,
即5﹕S△CDF=(1﹕3)2
∴S△CDF=45 cm2.
点评 本题考查了相似三角形的判定和性质以及平行四边形的判定,熟记相似三角形的各种性质是解题关键.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
6.大家知道:“距离地面越远,温度越低”.小明查阅资料得到下面表格中的对应数据:
根据表中,请你帮助小明解决下列问题:
(1)根据表格中的数据发现:距离地面高度每升高1km,温度就降低6℃,进而猜想:温度T与距离地面高度h之间的函数关系式为T=20-6h.
(2)当h=10km时,高空的温度T是多少?
(3)当T=-28℃时,距离地面的高度h是多少?
| 距离地面高度h/km | 0 | 1 | 2 | 3 | 4 | 5 | … |
| 温度T/℃ | 20 | 14 | 8 | 2 | -4 | -10 | … |
(1)根据表格中的数据发现:距离地面高度每升高1km,温度就降低6℃,进而猜想:温度T与距离地面高度h之间的函数关系式为T=20-6h.
(2)当h=10km时,高空的温度T是多少?
(3)当T=-28℃时,距离地面的高度h是多少?
20.下列计算结果为负数的是( )
| A. | |-3| | B. | (-3)0 | C. | -(+3) | D. | (-3)2 |
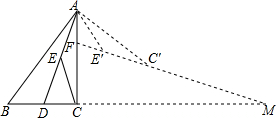 在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AD平分∠CAB交BC于点D,E为AD的中点,连接CE,将△ACE绕点A逆时针旋转至△AE′C′,直线E′C′交AC于点F,交BC的延长线于点M,若AF=E′F,则CM=$\frac{96-10\sqrt{10}}{7}$.
在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AD平分∠CAB交BC于点D,E为AD的中点,连接CE,将△ACE绕点A逆时针旋转至△AE′C′,直线E′C′交AC于点F,交BC的延长线于点M,若AF=E′F,则CM=$\frac{96-10\sqrt{10}}{7}$. 如图,在?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线BD、AC交于点O.将直线AC绕点O顺时针旋转分别交BC、AD于点E、F.
如图,在?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线BD、AC交于点O.将直线AC绕点O顺时针旋转分别交BC、AD于点E、F.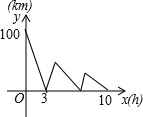 甲、乙两车分别从A、B两地同时出发,相向而行,甲车从A地行驶到B地后,立即按原速度返回A地,乙车从B地行驶到A地,两车到达A地均停止运动.两车之间的距离y(单位:千米)与乙车行驶时间x(单位:小时)之间的函数关系如图所示,问两车第二次相遇时乙车行驶的时间为$\frac{15}{2}$小时.
甲、乙两车分别从A、B两地同时出发,相向而行,甲车从A地行驶到B地后,立即按原速度返回A地,乙车从B地行驶到A地,两车到达A地均停止运动.两车之间的距离y(单位:千米)与乙车行驶时间x(单位:小时)之间的函数关系如图所示,问两车第二次相遇时乙车行驶的时间为$\frac{15}{2}$小时.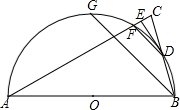 如图,已知△ABC中,AB=AC,∠A=30°,AB=16,以AB为直径的⊙O与BC边相交于点D,与AC交于点F,过点D作DE⊥AC于点E.
如图,已知△ABC中,AB=AC,∠A=30°,AB=16,以AB为直径的⊙O与BC边相交于点D,与AC交于点F,过点D作DE⊥AC于点E.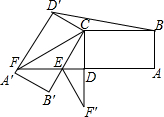 如图在矩形ABCD中,AB=4,将矩形ABCD绕点C顺时针旋转,得到矩形A′B′CD′,AD的延长线分别与B′C、A′D交于点E、F,使CE=2B′E,连接CF,将△CEF沿直线B′C折叠得到△CEF′,当CF′恰好经过点D时,则在△BCD′中以BD′为底的高为$\frac{2\sqrt{21}}{7}$.
如图在矩形ABCD中,AB=4,将矩形ABCD绕点C顺时针旋转,得到矩形A′B′CD′,AD的延长线分别与B′C、A′D交于点E、F,使CE=2B′E,连接CF,将△CEF沿直线B′C折叠得到△CEF′,当CF′恰好经过点D时,则在△BCD′中以BD′为底的高为$\frac{2\sqrt{21}}{7}$.